题目内容
在A处的甲船测得乙船在北偏西49°48′的B处,以速度22里/小时向正北方向行驶,甲船立即从A处出发,以速度26里/小时向北偏西α度的方向沿直线驶去追赶乙船,问α是多大角度时,经过一段时间甲船能够在某C处恰好与乙船相遇?(lg2.2=0.3424,lg2.6=0.4150)
分析:先设经过x小时后甲船在C处追上以船,则根据题意可知BC=22x,AC=26x进而根据正弦定理得sin(49°48′-α)=
,两边取对数,求得α
| 22•sin49°48′ |
| 26 |
解答:解:设经过x小时后,
甲船在C处追上以船,
则BC=22x(里)
AC=26x(里)
由正弦定理
=
,
即
=
∴sin(49°48′-α)=
,
取对数得lgsin(49°48′-α)=lg22+lgsin49°48′-lg26=
.8104,
49°48′-α=40°15′,
∴α=49°48′-40°15′=9°33′.
甲船在C处追上以船,
则BC=22x(里)
AC=26x(里)
由正弦定理
| BC |
| sin∠CAB |
| AC |
| sin∠ABC |
即
| 22x |
| sin(49°48′-α) |
| 26x |
| sin(180°-49°48′) |
∴sin(49°48′-α)=
| 22•sin49°48′ |
| 26 |
取对数得lgsin(49°48′-α)=lg22+lgsin49°48′-lg26=
. |
| 1 |
49°48′-α=40°15′,
∴α=49°48′-40°15′=9°33′.
点评:本题主要考查了正弦定理在实际中的应用.属基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,某海域中有甲、乙两艘测量船分别停留在相距(
如图,某海域中有甲、乙两艘测量船分别停留在相距(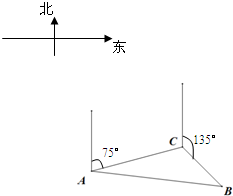 如图,甲船在A处测得:“乙船位于北偏东75°,距离为10海里的C处,并正沿着北偏东135°的方向,以每小时12海里的速度驶去.”经过半小时,甲船在B处追上了乙船.求:
如图,甲船在A处测得:“乙船位于北偏东75°,距离为10海里的C处,并正沿着北偏东135°的方向,以每小时12海里的速度驶去.”经过半小时,甲船在B处追上了乙船.求: