题目内容
已知函数 (0<φ<π,ω>0)为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
(0<φ<π,ω>0)为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为 .
.
(Ⅰ)求ω和φ的值;
(Ⅱ)将函数y=f(x)的图象向右平移 个单位后,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,得到函数y=g(x)的图象,求g(x)的单调递减区间.
解:(Ⅰ) =
= =
= .-------(2分)
.-------(2分)
因为f(x)为偶函数,
所以 ,即
,即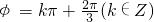 .
.
又因为0<φ<π,故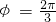 .--------(4分)
.--------(4分)
所以 .
.
由题意得 ,所以ω=2.---------(6分)
,所以ω=2.---------(6分)
(Ⅱ)由知f(x)=2cos2x,
所以 .--------(9分)
.--------(9分)
由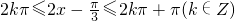 ,解得
,解得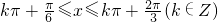 ,
,
因此g(x)的单调递减区间为 .----(12分)
.----(12分)
分析:(Ⅰ)利用辅助角公式可将f(x)= sin(ωx+φ)-cos(ωx+φ)(0<φ<π,ω>0)转化为f(x)=2sin(ωx+φ-
sin(ωx+φ)-cos(ωx+φ)(0<φ<π,ω>0)转化为f(x)=2sin(ωx+φ- ),为偶函数,?φ=kπ+
),为偶函数,?φ=kπ+ ,0<φ<π,可确定φ的值;又y=f(x)图象的两相邻对称轴间的距离为
,0<φ<π,可确定φ的值;又y=f(x)图象的两相邻对称轴间的距离为 ,从而求得ω;
,从而求得ω;
(Ⅱ)f(x)=2cos2x?g(x)=f(x- )=2cos(2x-
)=2cos(2x- ),由
),由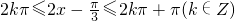 即可得g(x)的单调递减区间.
即可得g(x)的单调递减区间.
点评:本题考查函数y=Asin(ωx+φ)的图象变换,关键是用好辅助角公式,将f(x)= sin(ωx+φ)-cos(ωx+φ)(0<φ<π,ω>0)转化为f(x)=2sin(ωx+φ-
sin(ωx+φ)-cos(ωx+φ)(0<φ<π,ω>0)转化为f(x)=2sin(ωx+φ- ),再由其奇偶性与周期确定φ的值,重点考查三角函数的平移变换与单调性,属于中档题.
),再由其奇偶性与周期确定φ的值,重点考查三角函数的平移变换与单调性,属于中档题.
 =
= =
= .-------(2分)
.-------(2分)因为f(x)为偶函数,
所以
 ,即
,即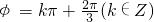 .
.又因为0<φ<π,故
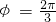 .--------(4分)
.--------(4分)所以
 .
.由题意得
 ,所以ω=2.---------(6分)
,所以ω=2.---------(6分)(Ⅱ)由知f(x)=2cos2x,
所以
 .--------(9分)
.--------(9分)由
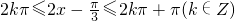 ,解得
,解得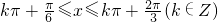 ,
,因此g(x)的单调递减区间为
 .----(12分)
.----(12分)分析:(Ⅰ)利用辅助角公式可将f(x)=
 sin(ωx+φ)-cos(ωx+φ)(0<φ<π,ω>0)转化为f(x)=2sin(ωx+φ-
sin(ωx+φ)-cos(ωx+φ)(0<φ<π,ω>0)转化为f(x)=2sin(ωx+φ- ),为偶函数,?φ=kπ+
),为偶函数,?φ=kπ+ ,0<φ<π,可确定φ的值;又y=f(x)图象的两相邻对称轴间的距离为
,0<φ<π,可确定φ的值;又y=f(x)图象的两相邻对称轴间的距离为 ,从而求得ω;
,从而求得ω;(Ⅱ)f(x)=2cos2x?g(x)=f(x-
 )=2cos(2x-
)=2cos(2x- ),由
),由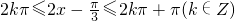 即可得g(x)的单调递减区间.
即可得g(x)的单调递减区间.点评:本题考查函数y=Asin(ωx+φ)的图象变换,关键是用好辅助角公式,将f(x)=
 sin(ωx+φ)-cos(ωx+φ)(0<φ<π,ω>0)转化为f(x)=2sin(ωx+φ-
sin(ωx+φ)-cos(ωx+φ)(0<φ<π,ω>0)转化为f(x)=2sin(ωx+φ- ),再由其奇偶性与周期确定φ的值,重点考查三角函数的平移变换与单调性,属于中档题.
),再由其奇偶性与周期确定φ的值,重点考查三角函数的平移变换与单调性,属于中档题. 
练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
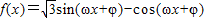 (0<φ<π,ω>0)为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
(0<φ<π,ω>0)为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为 .
.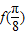 的值;
的值;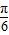 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.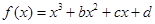 在(-
在(-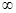 ,0)上是增函数,在[0,2]上是减函数,且方程
,0)上是增函数,在[0,2]上是减函数,且方程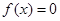 有三个根分别为
有三个根分别为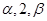 .
.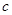 的值;
的值;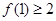 ;
;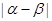 的取值范围.
的取值范围.  在[0,+
在[0,+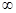 )上最小值是
)上最小值是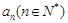
 的通项公式;
的通项公式; ,求证:
,求证: ;
; 在[0,1]上是减函数,则a的取值范围是( )
在[0,1]上是减函数,则a的取值范围是( ) B.(1,2) C.
B.(1,2) C. D.
D.
