题目内容
(本小题满分14分)已知双曲线
 (
( ,
, ),
), 、
、 分别是它的左、右焦点,
分别是它的左、右焦点, 是其左顶点,且双曲线的离心率为
是其左顶点,且双曲线的离心率为 .设过右焦点
.设过右焦点 的直线
的直线 与双曲线
与双曲线 的右支交于
的右支交于 、
、 两点,其中点
两点,其中点 位于第一象限内.
位于第一象限内.
(1)求双曲线的方程;
(2)若直线 、
、 分别与直线
分别与直线 交于
交于 、
、 两点,求证:
两点,求证: ;
;
(3)是否存在常数 ,使得
,使得 恒成立?若存在,求出
恒成立?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(1)
(2)见解析
(3)见解析
【解析】
试题分析:(1)【解析】
由题可知: 1分
1分
∵ ,∴c=2 2分
,∴c=2 2分
∵ ,∴
,∴ ,
,
∴双曲线C的方程为: 3分
3分
(2)证明:设直线 的方程为:x=ty+2,另设:
的方程为:x=ty+2,另设: ,
, ,
,
∴ , 4分
, 4分
∴ 5分
5分
又直线AP的方程为 ,代入
,代入 6分
6分
同理,直线AQ的方程为 ,代入
,代入 7分
7分
∴ ,
,
∴
 ,∴
,∴ 9分
9分
(3)【解析】
当直线 的方程为
的方程为 时,解得P(2,3),
时,解得P(2,3),
易知此时 为等腰直角三角形,其中
为等腰直角三角形,其中 ,
,
即 ,也即:
,也即: 10分
10分
下证: 对直线
对直线 存在斜率的情形也成立,
存在斜率的情形也成立,
 , 11分
, 11分
∵ ,
,
∴ , 12分
, 12分
∴ 13分
13分
∴结合正切函数在 上的图像可知,
上的图像可知, 14分
14分
考点:考查了双曲线的方程,直线与双曲线的位置关系.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
 B.
B.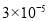 C.
C.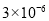 D.
D.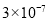

 B.
B. C.
C. D.
D.
 在点
在点 处的切线方程为 .
处的切线方程为 . ,
, 满足约束条件
满足约束条件 ,则
,则 的最大值等于( )
的最大值等于( ) B.
B. C.
C. D.
D.
 是圆
是圆 的直径,点
的直径,点 在圆
在圆 上,延长
上,延长 到
到 使
使 ,过
,过 作圆
作圆 的切线交
的切线交 于
于 .若
.若 ,
, ,则
,则 .
.
 ,集合
,集合 .令集合
.令集合 .若
.若 和
和 都在
都在 中,则下列选项正确的是( )
中,则下列选项正确的是( ) ,
,
 ,
,
 ,
,
 ,
,
 ,则
,则 __________.
__________. ,B(5,1),则以线段AB为直径的圆的方程的一般式为 .
,B(5,1),则以线段AB为直径的圆的方程的一般式为 .