题目内容
平面四边形ABCD中
+
=
，(
-
) •
=0，则四边形ABCD是（ ）
| AB |
| CD |
| 0 |
| AB |
| AD |
| AC |
分析：根据
+
=
，得线段AB、CD平行且相等，所以四边形ABCD是平行四边形．再由(
-
) •
=0，得
对角线AC、BD互相垂直，即可得到四边形ABCD是菱形．
| AB |
| CD |
| 0 |
| AB |
| AD |
| AC |
对角线AC、BD互相垂直，即可得到四边形ABCD是菱形．
解答：解：∵
+
=
，
∴
=-
即
=
，可得线段AB、CD平行且相等
∴四边形ABCD是平行四边形
又∵(
-
) •
=0，
∴
-
⊥
，即
⊥
，四边形ABCD的对角线互相垂直
因此四边形ABCD是菱形
故选：B
| AB |
| CD |
| 0 |
∴
| AB |
| CD |
| AB |
| DC |
∴四边形ABCD是平行四边形
又∵(
| AB |
| AD |
| AC |
∴
| AB |
| AD |
| AC |
| DB |
| AC |
因此四边形ABCD是菱形
故选：B
点评：本题给出向量条件，判断四边形ABCD的形状，着重考查了平面向量的线性运算、数量积运算及其性质，考查了菱形的判定方法，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
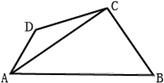如图，平面四边形ABCD中，AB=13，三角形ABC的面积为S△ABC=25，
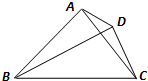如图，在平面四边形ABCD中，若AB=2，CD=1，则
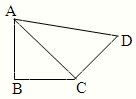如图，在平面四边形ABCD中，AB=BC=CD=a，∠ABC=90°，∠BCD=135°，沿对角线AC将此四边形折成直二面角．
如图甲，在平面四边形ABCD中，已知∠A=45°，∠C=90°，AB=BD=2CD，现将四边形ABCD沿BD折起，使平面ABD⊥平面BDC（如图乙），设点E为棱AD的中点．