题目内容
19.已知一圆C的圆心为C(2,-1),且该圆被直线l:x-y-1=0截得的弦长是2$\sqrt{2}$,求该圆的方程和过弦两端点的切线的方程.分析 设圆C的方程是(x-2)2+(y+1)2=r2(r>0),利用圆的半径、弦心距及弦长的关系求得r,则圆的方程可求;画出图形,联立直线方程和圆的方程,求出弦的两端点的坐标,即可得到过弦两端点的切线的方程.
解答 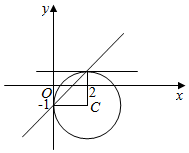 解:设圆C的方程是(x-2)2+(y+1)2=r2(r>0),
解:设圆C的方程是(x-2)2+(y+1)2=r2(r>0),
则弦长P=2$\sqrt{{r}^{2}-{d}^{2}}$,
其中d为圆心到直线x-y-1=0的距离,d=$\frac{|2×1+1-1|}{\sqrt{2}}=\sqrt{2}$
∴P=2$\sqrt{{r}^{2}-(\sqrt{2})^{2}}=2\sqrt{2}$,则r2=4,
∴圆的方程为(x-2)2+(y+1)2=4;
如图,
联立$\left\{\begin{array}{l}{y=x-1}\\{(x-2)^{2}+(y+1)^{2}=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=0}\\{y=-1}\end{array}\right.$或$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$.
∴弦的两个端点为(0,-1),(2,1),
由图可知,过点(0,-1)的切线方程为x=0;
过点(2,1)的切线方程为y=1.
点评 本题考查圆的方程与圆的切线方程的求法,考查数形结合的解题思想方法,注意圆的性质的合理运用,是中档题.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
14.命题“p或q”为真命题( )
| A. | 命题p为真 | B. | 命题q为真 | ||
| C. | 命题p和命题q一真一假 | D. | 命题p和命题q至少一个为真 |