题目内容
19.已知幂函数y=xa的图象过点(3,9),则${(\frac{a}{x}-\sqrt{x})}^{8}$的展开式中x的系数为112.分析 直接利用幂函数求出a的值,然后求出二项式展开式中所求项的系数.
解答 解:幂函数y=xa的图象过点(3,9),
∴3a=9,
∴a=2,
∴${(\frac{a}{x}-\sqrt{x})}^{8}$=($\frac{2}{x}$-$\sqrt{x}$)8的通项为Tr+1=(-1)rC8r28-rx${\;}^{\frac{3}{2}r-8}$,
令$\frac{3}{2}$r-8=1,
解得r=6,
展开式中x的系数为(-1)6C8628-6=112,
故答案为:112.
点评 本题考查二项式定理的应用,幂函数的应用,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.已知命题p:若x>10,则x>1,那么p的逆否命题为( )
| A. | 若x>1,则x>10 | B. | 若x>10,则x≤1 | C. | 若x≤10,则x≤1 | D. | 若x≤1,则x≤10 |
8.已知函数f(x)=ax3+(3-a)x在[-1,1]上的最大值为3,则实数a的取值范围是( )
| A. | [-$\frac{3}{2}$,3] | B. | [-$\frac{3}{2}$,12] | C. | [-3,3] | D. | [-3,12] |
9.已知全集U={x|x=2n,n∈Z},集合A={-2,0,2,4},B={-2,0,4,6,8},则∁UA)∩B=( )
| A. | {2,8} | B. | {6,8} | C. | {2,4,6} | D. | {2,4,8} |
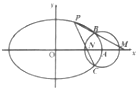 已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的长轴长为4,焦距为$2\sqrt{3}$,以A为圆心的圆(x-2)2+y2=r2(r>0)与椭圆相交于B、C两点.
已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的长轴长为4,焦距为$2\sqrt{3}$,以A为圆心的圆(x-2)2+y2=r2(r>0)与椭圆相交于B、C两点.