题目内容
已知数列 满足
满足 .
.
(I)求证:当 时,数列
时,数列 为等比数列;
为等比数列;
(II)如果 ,求数列
,求数列 的前n项和
的前n项和 ;
;
(III)如果 表示不超过
表示不超过 的最大整数,当
的最大整数,当 时,求数列
时,求数列 的通项公式.
的通项公式.
解:(I)当 时,设
时,设 ,
,
则当 时,
时, .
.
因为 ,
,
所以 为常数.
为常数.
因为 ,
,
所以,数列 是首项为
是首项为 ,公比为
,公比为 的等比数列.
的等比数列.
(II)由(I)知 时
时 为首项为
为首项为 ,公比为
,公比为 的等比数列,
的等比数列,
所以 ,
, .
.
设 ,
,
则 .
.
相减得 .
.
设 ,
, .
.
即 .
.
(III)由(I)可知 .
.
设 ,
,
由二项式定理可知 为整数.
为整数.
所以 .
.
所以 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,
中, ,
, ,
, ,设点
,设点 ,满足
,满足

 .若
.若 ,则
,则 的值是 .
的值是 .  ,
, 满足约束条件
满足约束条件 则
则 的最大值是 .
的最大值是 .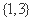 (B)
(B)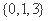 (C)
(C)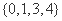 (D)
(D)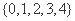
 .
. 的最小正周期;
的最小正周期; 上的最大值和最小值及相应的
上的最大值和最小值及相应的 的值.
的值.



 表示的平面区域为
表示的平面区域为 . 则区域
. 则区域 是
是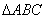 的重心,
的重心, ,则
,则 ( )
( ) B.
B.
 D.
D.

 ,BC
,BC ,点E为BC的中点,点F在CD上,若
,点E为BC的中点,点F在CD上,若 ,则
,则 的值是( )
的值是( ) B.
B. C.
C. D.
D.
