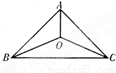
题目内容
设(| OB |
| OA |
| OC |
分析:利用向量共线的充要条件:
=λ
列出等式再利用向量减法法则将等式用
,
,
表示;利用平面向量基本定理对应的系数相等得到x+y.
| a |
| b |
| OA |
| OB |
| OC |
解答:解:∵A、B、C三点共线,
∴存在一个实数λ,
=λ
即(
)-(
)=λ((
)-(
)).
(
)=(1-λ)(
)+λ(
).
又∵(
)=x(
)+y(
),
∴x+y=(1-λ)+λ=1.
故答案为1
∴存在一个实数λ,
| AB |
| AC |
| OB |
| OA |
| OC |
| OA |
(
| OB |
| OA |
| OC |
又∵(
| OB |
| OA |
| OC |
∴x+y=(1-λ)+λ=1.
故答案为1
点评:本题考查两个
,
共线的充要条件是
=λ
(
≠
)
| a |
| b |
| a |
| b |
| b |
| 0 |

练习册系列答案
相关题目
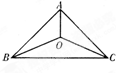 三个城市襄阳、荆州、武汉分别位于A,B,C三点处(如右图),且
三个城市襄阳、荆州、武汉分别位于A,B,C三点处(如右图),且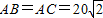 km,BC=40km.今计划合建一个货运中转站,为同时方便三个城市,准备建在与B、C等距离的O点处,并修建道路OA,OB,OC.记修建的道路的总长度为ykm.
km,BC=40km.今计划合建一个货运中转站,为同时方便三个城市,准备建在与B、C等距离的O点处,并修建道路OA,OB,OC.记修建的道路的总长度为ykm.