题目内容
12.若函数f(x)=2|x-a|(a∈R)满足f(1+x)=f(1-x),且f(x)在[m,+∞)上单调递增,则实数m的最小值等于1.分析 根据式子f(1+x)=f(1-x),对称f(x)关于x=1对称,利用指数函数的性质得出:函数f(x)=2|x-a|(a∈R),x=a为对称轴,在[1,+∞)上单调递增,即可判断m的最小值.
解答 解:∵f(1+x)=f(1-x),
∴f(x)关于x=1对称,
∵函数f(x)=2|x-a|(a∈R)
x=a为对称轴,
∴a=1,
∴f(x)在[1,+∞)上单调递增,
∵f(x)在[m,+∞)上单调递增,
∴m的最小值为1.
故答案为:1.
点评 本题考查了指数型函数的单调性,对称性,根据函数式子对称函数的性质是本题解决的关键,难度不大,属于中档题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
2.设双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右焦点为F,右顶点为A,过F作AF的垂线与双曲线交于B,C两点,过B,C分别作AC,AB的垂线,两垂线交于点D.若D到直线BC的距离小于a+$\sqrt{{a^2}+{b^2}}$,则该双曲线的渐近线斜率的取值范围是( )
| A. | (-1,0)∪(0,1) | B. | (-∞,-1)∪(1,+∞) | C. | (-$\sqrt{2}$,0)∪(0,$\sqrt{2}$) | D. | (-∞,-$\sqrt{2}$)∪($\sqrt{2}$,+∞) |
3.一辆小客车上有5名座位,其座号为1,2,3,4,5,乘客P1,P2,P3,P4,P5的座位号分别为1,2,3,4,5.他们按照座位号顺序先后上车,乘客P1因身体原因没有坐自己1号座位,这时司机要求余下的乘客按以下规则就坐:如果自己的座位空着,就只能坐自己的座位.如果自己的座位已有乘客就坐,就在这5个座位的剩余空位中选择座位.
(Ⅰ)若乘客P1坐到了3号座位,其他乘客按规则就座,则此时共有4种坐法.下表给出其中两种坐法,请填入余下两种坐法(将乘客就坐的座位号填入表中空格处)
(Ⅱ)若乘客P1坐到了2号座位,其他乘客按规则就坐,求乘客P5坐到5号座位的概率.
(Ⅰ)若乘客P1坐到了3号座位,其他乘客按规则就座,则此时共有4种坐法.下表给出其中两种坐法,请填入余下两种坐法(将乘客就坐的座位号填入表中空格处)
| 乘客 | P1 | P2 | P3 | P4 | P5 |
| 座位号 | 3 | 2 | 1 | 4 | 5 |
| 3 | 2 | 4 | 5 | 1 | |
| 3 | 2 | 4 | 1 | 5 | |
| 3 | 2 | 5 | 4 | 1 |
20.若集合M={x|-2≤x<2},N={0,1,2},则M∩N=( )
| A. | {0} | B. | {1} | C. | {0,1,2} | D. | {0,1} |
7.某几何体的三视图如图所示,则该几何体的表面积等于( )
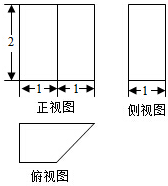

| A. | 8+2$\sqrt{2}$ | B. | 11+2$\sqrt{2}$ | C. | 14+2$\sqrt{2}$ | D. | 15 |
4.若变量x,y满足约束条件$\left\{\begin{array}{l}x+2y≥0\\ x-y≤0\\ x-2y+2≥0\end{array}\right.$则z=2x-y的最小值等于( )
| A. | $-\frac{5}{2}$ | B. | -2 | C. | $-\frac{3}{2}$ | D. | 2 |
 如图,AB是圆O的直径,点C是圆O上异于A,B的点,PO垂直于圆O所在的平面,且PO=OB=1,
如图,AB是圆O的直径,点C是圆O上异于A,B的点,PO垂直于圆O所在的平面,且PO=OB=1,