题目内容
7.某几何体的三视图如图所示,则该几何体的表面积等于( )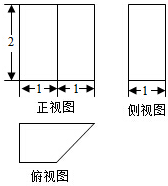
| A. | 8+2$\sqrt{2}$ | B. | 11+2$\sqrt{2}$ | C. | 14+2$\sqrt{2}$ | D. | 15 |
分析 判断出该几何体是底面为直角梯形,高为2的直四棱柱,底面的梯形上底1,下底2,高为1,运用梯形,矩形的面积公式求解即可.
解答 解:根据三视图可判断该几何体是底面为直角梯形,高为2的直四棱柱,
底面的梯形上底1,下底2,高为1,
∴侧面为(4$+\sqrt{2}$)×2=8$+2\sqrt{2}$,
底面为$\frac{1}{2}×$(2+1)×1=$\frac{3}{2}$,
故几何体的表面积为8$+2\sqrt{2}$$+2×\frac{3}{2}$=11$+2\sqrt{2}$,
故选:B.
点评 本题考查了空间几何体的三视图的运用,空间想象能力,关键是能够恢复判断几何体的形状.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
17.“x>1”是“$lo{g_{\frac{1}{2}}}$(x+2)<0”的( )
| A. | 充要条件 | B. | 充分而不必要条件 | ||
| C. | 必要而不充分条件 | D. | 既不充分也不必要条件 |
18.某食品保鲜时间y(单位:小时)与储藏温度x(单位:℃)满足函数关系y=ekx+b (e=2.718…为自然对数的底数,k,b为常数).若该食品在0℃的保鲜时间是192小时,在22℃的保鲜时间是48小时,则该食品在33℃的保鲜时间是( )
| A. | 16小时 | B. | 20小时 | C. | 24小时 | D. | 28小时 |
2.阅读如图所示的程序框图,运行相应的程序,若输入x的值为1,则输出y的值为( )
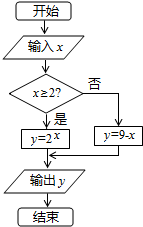

| A. | 2 | B. | 7 | C. | 8 | D. | 128 |
17. 如图,斜线段AB与平面α所成的角为60°,B为斜足,平面α上的动点P满足∠PAB=30°,则点P的轨迹是( )
如图,斜线段AB与平面α所成的角为60°,B为斜足,平面α上的动点P满足∠PAB=30°,则点P的轨迹是( )
 如图,斜线段AB与平面α所成的角为60°,B为斜足,平面α上的动点P满足∠PAB=30°,则点P的轨迹是( )
如图,斜线段AB与平面α所成的角为60°,B为斜足,平面α上的动点P满足∠PAB=30°,则点P的轨迹是( )| A. | 直线 | B. | 抛物线 | C. | 椭圆 | D. | 双曲线的一支 |

 线段BE,DC的中点.
线段BE,DC的中点.