Question

【题目】已知函数 （a∈R）． （Ⅰ）当 时，求f（x）的单调区间；
（Ⅱ）若 对任意的x＞0恒成立，求a的取值范围．

Answer 1

【答案】解：（Ⅰ）当 时，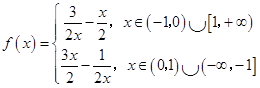

所以f（x）的单调递增区间是（0，1]，（﹣∞，﹣1]，

单调递减区间是[1，+∞），[﹣1，0）

（Ⅱ）由 得 ，

∴

①当0＜x＜1时， ，

∴

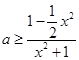
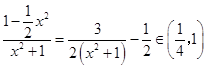∵ ∴a≥1

②当x＞1时， ，

∴

∵ ，

∴

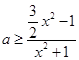
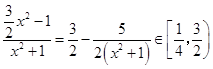综上所述，a的取值范围是

【解析】（Ⅰ）将a的值带入f（x），求出f（x）的解析式，从而求出f（x）的单调区间即可；（Ⅱ）通过讨论x的范围，去掉绝对值号，分离参数a，从而求出a的范围即可．
【考点精析】认真审题，首先需要了解利用导数研究函数的单调性(一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减)，还要掌握函数的最大(小)值与导数(求函数在上的最大值与最小值的步骤：（1）求函数在内的极值；（2）将函数的各极值与端点处的函数值，比较，其中最大的是一个最大值，最小的是最小值)的相关知识才是答题的关键．