题目内容
直线l1：2x+y-3=0与直线l2：
的夹角是
- A.arctan3
- B.π-arctan3
- C.
- D.
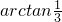
A
分析：先根据两直线的方程求出两直线的斜率，代入两条直线的夹角公式tanθ=|
|，求出θ的值．
解答：直线2x+y-3=0与直线y=x-
的斜率分别为-2、1，
设直线l1：2x+y-3=0与直线l2：的夹角是θ，则有 tanθ=||=|
|=3．
再由 0≤θ≤
可得 θ=arctan3．
故选：A．
点评：本题主要考查两条直线的夹角公式，求出两直线的斜率，是解题的突破口．
分析：先根据两直线的方程求出两直线的斜率，代入两条直线的夹角公式tanθ=|
|，求出θ的值．解答：直线2x+y-3=0与直线y=x-
的斜率分别为-2、1，设直线l1：2x+y-3=0与直线l2：
的夹角是θ，则有 tanθ=||=||=3．再由 0≤θ≤
可得 θ=arctan3．故选：A．
点评：本题主要考查两条直线的夹角公式，求出两直线的斜率，是解题的突破口．
练习册系列答案
相关题目
已知直线l1：2x-y+3=0，l2：
x+y-5=0，l3：3x-2y=0的倾斜角分别是α1、α2、α3则α1、α2、α3的大小关系是（ ）
| 3 |
| A、α1＞α2＞α3 |
| B、α2＞α1＞α3 |
| C、α1＞α3＞α2 |
| D、α3＞α1＞α |
（2011•广东模拟）如果直线l1：2x-y+2=0，l2：8x-y-4=0与x轴正半轴，y轴正半轴围成的四边形封闭区域（含边界）中的点，使函数z=abx+y（a＞0，b＞0）的最大值为8，求a+b的最小值．