题目内容
【题目】对于定义域为![]() 的函数
的函数![]() ,若满足①
,若满足①![]() ;②当
;②当![]() ,且
,且![]() 时,都有
时,都有![]() ;③当
;③当![]() ,且
,且![]() 时,都有
时,都有![]() ,则称
,则称![]() 为“偏对称函数”.现给出四个函数:
为“偏对称函数”.现给出四个函数:![]() ;
;![]() ;
;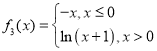 ;
;![]() .则其中是“偏对称函数”的函数个数为( )
.则其中是“偏对称函数”的函数个数为( )
A.3B.2C.1D.0
【答案】D
【解析】
条件②等价于![]() 在(∞,0)上单调递减,在(0,+∞)上单调递增,条件③等价于
在(∞,0)上单调递减,在(0,+∞)上单调递增,条件③等价于![]() 在(∞,0)上恒成立,依次判断各函数是否满足条件即可得出结论.
在(∞,0)上恒成立,依次判断各函数是否满足条件即可得出结论.
解:由②可知当x>0时,![]() ,当x<0时,
,当x<0时,![]() ,
,
∴![]() 在(∞,0)上单调递减,在(0,+∞)上单调递增;
在(∞,0)上单调递减,在(0,+∞)上单调递增;
由③可知当![]() 时,
时,![]() ,即
,即![]() 在(∞,0)上恒成立;
在(∞,0)上恒成立;
对![]() ,
,
有![]() ,
,
∴![]() 在(∞,-1)上单调递减,在(-1,+∞)上单调递增,故
在(∞,-1)上单调递减,在(-1,+∞)上单调递增,故![]() 不满足条件②,
不满足条件②,
∴![]() 不是“偏对称函数”;
不是“偏对称函数”;
对![]() ,
,
有![]() ,
,
∴![]() 是奇函数,在R上单调递增,不满足条件②,
是奇函数,在R上单调递增,不满足条件②,
∴![]() 不是“偏对称函数”;
不是“偏对称函数”;
对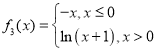 ,
,
当![]() 时,
时,![]() ,
,
令![]() ,则
,则![]() ,
,
∴![]() 在(∞,0)上单调递减,故
在(∞,0)上单调递减,故![]() ,不满足条件③,
,不满足条件③,
∴![]() 不为“偏对称函数”;
不为“偏对称函数”;
对![]() ,
,
![]() ,令
,令![]() ,得
,得![]() ,
,
则![]() 在(∞,
在(∞,![]() )上单调递减,在(
)上单调递减,在(![]() ,+∞)上单调递增,故
,+∞)上单调递增,故![]() 不满足条件②,
不满足条件②,
∴![]() 不为“偏对称函数”.
不为“偏对称函数”.
故选:D.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目