Question

【题目】设二次函数（，），关于的不等式的解集中有且只有一个元素.

（1）设数列的前项和（），求数列的通项公式；

（2）设（），则数列中是否存在不同的三项能组成等比数列？请说明理由.

Answer 1

【答案】(1) 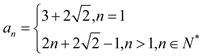,(2)见解析

【解析】

（1）由等式的解集中有且只有一个元素可利用判别式等于0算出，，有关通项与前项和的等式，一般先令，再利用，，推导的通项公式即可。
（2）求出的通项公式，利用等比数列的性质，建立等式即可分析得出结论。

（1）因为关于的不等式的解集中有且只有一个元素，

所以二次函数的图象与轴相切，

于是，考虑到，所以.

从而，故数列的前项和.

于是；

当时，.

故数列的通项公式为．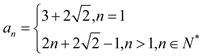

（2）.

假设数列中存在三项（正整数互不相等）成等比数列，

则，即，

整理得.

因为都是正整数，所以，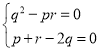

于是，即，从而与矛盾.

故数列中不存在不同三项能组成等比数列.