题目内容
设矩形ABCD（AB>AD）的周长为12。把它关于AC折起来，AB折过后交DC于点P，设AB=x，求△ADP的最大面积及相应的x的值。
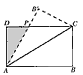
解：因为AB=x，所以AD=6-x，
由AB>AD，∴x>6-x>0，
∴3<x<6，
又AP=AB′-PB′=AB-DP=x-DP，
在Rt△ADP中，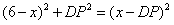
，
∴
，
∴
，
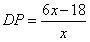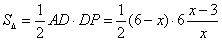
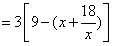
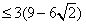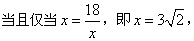
∴S有最大值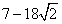
。
由AB>AD，∴x>6-x>0，
∴3<x<6，
又AP=AB′-PB′=AB-DP=x-DP，
在Rt△ADP中，
，∴
，∴
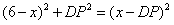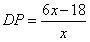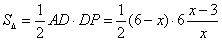
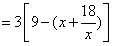
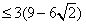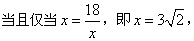
，∴S有最大值
。
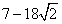练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
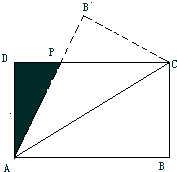设矩形ABCD（AB＞AD）的周长为12．把它关于AC折起来，AB折过后交DC于点P，设AB=x，求△ADP的最大面积及相应的x的值．
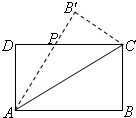如图，设矩形ABCD（AB＞AD）的周长为24，把它关于AC折起来，AB折过去后，交DC于P，设AB=x．
如图，设矩形ABCD（AB＞AD）的周长为4，把它关于AC折起来，AB折过去后，交DC与点P．设AB=x，求△ADP的最大面积及相应的x的值．
如图，设矩形ABCD（AB＞AD）的周长为l（l为定值），把该矩形沿AC折起来，AB折过去后，交DC于点P，设AB=x，△ADP的面积为y．
如图，设矩形ABCD（AB＞AD）的周长为24，把它关于AC折起来，AB折过去后，交DC于P，设AB=x，