题目内容
若函数y=xlnx+a有零点,则实数a的取值范围是 .
【答案】分析:利用导数求得当x=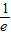 时,函数取得最小值,再根据函数的最小值小于或等于零,求得实数a的取值范围.
时,函数取得最小值,再根据函数的最小值小于或等于零,求得实数a的取值范围.
解答:解:由于函数的定义域为(0,+∞),令函数的导数y′=lnx+1=0,求得x=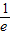 .
.
在(0,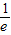 )上,y′<0,函数y是减函数,在(
)上,y′<0,函数y是减函数,在(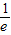 ,+∞)上,y′>0,函数y是增函数,故当x=
,+∞)上,y′>0,函数y是增函数,故当x=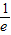 时,函数取得最小值.
时,函数取得最小值.
要使函数有零点,需函数的最小值小于或等于零,即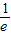 •ln
•ln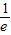 +a≤0,∴a≤
+a≤0,∴a≤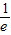 ,
,
即实数a的取值范围是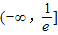 ,
,
故答案为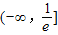 .
.
点评:本题主要考查利用导数研究函数的单调性,根据函数的单调性求函数的最值,函数有零点的条件,属于基础题.
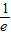 时,函数取得最小值,再根据函数的最小值小于或等于零,求得实数a的取值范围.
时,函数取得最小值,再根据函数的最小值小于或等于零,求得实数a的取值范围.解答:解:由于函数的定义域为(0,+∞),令函数的导数y′=lnx+1=0,求得x=
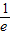 .
.在(0,
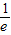 )上,y′<0,函数y是减函数,在(
)上,y′<0,函数y是减函数,在(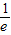 ,+∞)上,y′>0,函数y是增函数,故当x=
,+∞)上,y′>0,函数y是增函数,故当x=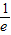 时,函数取得最小值.
时,函数取得最小值.要使函数有零点,需函数的最小值小于或等于零,即
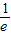 •ln
•ln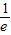 +a≤0,∴a≤
+a≤0,∴a≤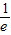 ,
,即实数a的取值范围是
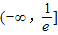 ,
,故答案为
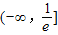 .
.点评:本题主要考查利用导数研究函数的单调性,根据函数的单调性求函数的最值,函数有零点的条件,属于基础题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目