题目内容
以双曲线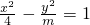 的离心率为半径,以右焦点为圆心的圆与该双曲线的渐近线相切,则m的值为
的离心率为半径,以右焦点为圆心的圆与该双曲线的渐近线相切,则m的值为
- A.

- B.

- C.

- D.

C
分析:因双曲线的焦点在x轴上,所以其右焦点坐标为(c,0),渐近线方程为y=± x,故满足要求的圆的半径为右焦点到渐近线的距离,因此只需根据点到直线的距离公式列方程求m即可.
x,故满足要求的圆的半径为右焦点到渐近线的距离,因此只需根据点到直线的距离公式列方程求m即可.
解答:由题意知,a2=4,b2=m,c2=m+4
圆的半径等于右焦点(c,0)到其中一条渐近线 y= x的距离,
x的距离,
根据点到直线的距离公式得:
R= .
.
解得:m=
故选C.
点评:本小题主要考查双曲线的简单性质、圆与圆锥曲线的综合、方程式的解法等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.
分析:因双曲线的焦点在x轴上,所以其右焦点坐标为(c,0),渐近线方程为y=±
 x,故满足要求的圆的半径为右焦点到渐近线的距离,因此只需根据点到直线的距离公式列方程求m即可.
x,故满足要求的圆的半径为右焦点到渐近线的距离,因此只需根据点到直线的距离公式列方程求m即可.解答:由题意知,a2=4,b2=m,c2=m+4
圆的半径等于右焦点(c,0)到其中一条渐近线 y=
 x的距离,
x的距离,根据点到直线的距离公式得:
R=
 .
.解得:m=

故选C.
点评:本小题主要考查双曲线的简单性质、圆与圆锥曲线的综合、方程式的解法等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
相关题目
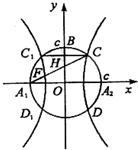 如图,以A1,A2为焦点的双曲线E与半径为c的圆O相交于C,D,C1,D1,连接CC1与OB交于点H,且有:
如图,以A1,A2为焦点的双曲线E与半径为c的圆O相交于C,D,C1,D1,连接CC1与OB交于点H,且有: 如图所示,双曲线的中心在原点,F、E分别是其左、右焦点,若双曲线的右支上存在一点P,满足以双曲线的虚半轴长为直径的圆与线段PF相切于其中点C,则该双曲线的离心率为
如图所示,双曲线的中心在原点,F、E分别是其左、右焦点,若双曲线的右支上存在一点P,满足以双曲线的虚半轴长为直径的圆与线段PF相切于其中点C,则该双曲线的离心率为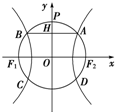 如图,双曲线
如图,双曲线