题目内容
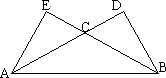
如图所示，双曲线的中心在原点，F、E分别是其左、右焦点，若双曲线的右支上存在一点P，满足以双曲线的虚半轴长为直径的圆与线段PF相切于其中点C，则该双曲线的离心率为 ．
【答案】分析：根据切线的性质和三角形中位线定理，证出△PEF中，PF⊥PE且|PE|=2b，用勾股定理算出|PF|=2a，结合双曲线的定义算出b=2a，c=
a．由此即可得出该双曲线的离心率．
解答：解：∵⊙O切直线PF于点C，∴0C⊥PF
∵0C是△PEF的中位线，得PE∥0C且|PE|=2|0C|
∴△PEF是以EF为斜边的直角三角形，|PE|=2b
由此可得：|PF|=
=
=2a
根据双曲线定义，得|PF|-|PE|=2a
∴2a-2b=2a，可得b=2a，c=
=
a
该双曲线的离心率为e=
=
故答案为：
点评：本题给出双曲线的一条焦半径与以虚轴为直径的圆相切于中点，求该双曲线的离心率．着重考查了直线与圆相切的性质、双曲线的定义与简单几何性质等知识，属于中档题．
a．由此即可得出该双曲线的离心率．解答：解：∵⊙O切直线PF于点C，∴0C⊥PF
∵0C是△PEF的中位线，得PE∥0C且|PE|=2|0C|
∴△PEF是以EF为斜边的直角三角形，|PE|=2b
由此可得：|PF|=
==2a根据双曲线定义，得|PF|-|PE|=2a
∴2a-2b=2a，可得b=2a，c=
=a该双曲线的离心率为e=
=故答案为：
点评：本题给出双曲线的一条焦半径与以虚轴为直径的圆相切于中点，求该双曲线的离心率．着重考查了直线与圆相切的性质、双曲线的定义与简单几何性质等知识，属于中档题．
练习册系列答案
相关题目
（2012•红桥区一模）如图所示，双曲线
（2008•宣武区一模）在面积为9的△ABC中，
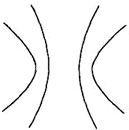已知定圆O1、O2的半径分别为r1、r2，圆心距|O1O2|=2，动圆C与圆O1、O2都相切，圆心C的轨迹为如图所示的两条双曲线，两条双曲线的离心率分别为e1、e2，则| e1+e2 |
| e1e2 |
| A、r1+r2 |
| B、r1和r2中的较大者 |
| C、r1和r2中的较小者 |
| D、|r1-r2| |
中，
，且
。现建立以A点为坐标原点，以
的平分线所在直线为x轴的平面直角坐标系，如图所示。
的值。