题目内容

设相交于G.，，且，所以如图，已知正方体ABCD—A1B1C1D1的棱长为a，求异面直线A1C1与BD1的距离.


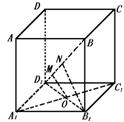
解析:

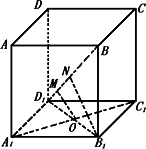
本题的关键是画出A1C1与BD1的公垂线，连B1D1交A1C1于O，在平面BB1D1内作OM⊥BD1，则OM就是A1C1与BD1的公垂线，问题得到解决.

解  连B1D1交A1C1于O，作OM⊥BD1于M.

∴  A1C1⊥B1D1，BB1⊥A1C1，BB1∩B1D1＝B1.

∴  A1C1⊥平面BB1D1.  ∴  A1C1⊥OM，又OM⊥BD1.

∴  OM是异面直线A1C1与BD1的公垂线.

在直角ΔBB1D1中作B1N⊥BD1于N.

∵  BB1·B1D1＝B1N·BD1，a·a＝B1N·a，

∴  B1N＝a,OM＝B1N＝a.

故异面直线A1C1与BD1的距离为a.

评析：作异面直线的公垂线一般是比较困难的，只有熟练地掌握线、线垂直，线、面垂直的关系后才能根据题目所给条件灵活作出.本题在求OM的长度时，主要运用中位线和面积的等量关系.

练习册系列答案
相关题目
在平行四边形OABC中，已知过点C的直线与线段OA，OB分别相交于点M，N．若
OM
=x
OA
，
ON
=y
OB
．
（1）求证：x与y的关系为y=
x
x+1
；
（2）设f(x)=
x
x+1
，定义函数F(x)=
1
f(x)
-1(0＜x≤1)，点列Pi（xi，F（xi））（i=1，2，…，n，n≥2）在函数F（x）的图象上，且数列{xn}是以首项为1，公比为
1
2
的等比数列，O为原点，令
OP
=
OP1
+
OP2
+…+
OPn
，是否存在点Q（1，m），使得
OP
⊥
OQ
？若存在，请求出Q点坐标；若不存在，请说明理由．
（3）设函数G（x）为R上偶函数，当x∈[0，1]时G（x）=f（x），又函数G（x）图象关于直线x=1对称，当方程G(x)=ax+
1
2
在x∈[2k，2k+2]（k∈N）上有两个不同的实数解时，求实数a的取值范围．
已知点A（-2，0），B（2，0），直线AG，BG相交于点G，且它们的斜率之积是-
14
．
（Ⅰ）求点G的轨迹Ω的方程；
（Ⅱ）圆x2+y2=4上有一个动点P，且P在x轴的上方，点C（1，0），直线PA交（Ⅰ）中的轨迹Ω于D，连接PB，CD．设直线PB，CD的斜率存在且分别为k1，k2，若k1=λk2，求实数λ的取值范围．

设A1C与C1O相交于G，∵A1C1∥AC，且A1C1∶OC＝2∶1，所以C1O：如图，已知正方体ABCD－A1B1C1D1的棱长为a，求异面直线A1C1与BD1的距离．

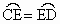如图，BC是半圆的直径，D、E是半圆上的两点，且．过C作半圆的切线，与BE的延长线相交于F，BE与CD相交于G，CE、BD的延长线相交于A，连结DE．

(1)求证：AB=BC；

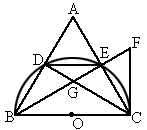
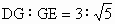(2)如果，BG=3k，试用含k的代数式表示AC；

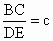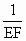(3)设FC=a，BF＋FC=b，，求证：是方程的根，并求出这个方程的另一个根．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网