Question

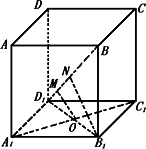
设A₁C与C₁O相交于G，∵A₁C₁∥AC，且A₁C₁∶OC＝2∶1，所以C₁O：如图，已知正方体ABCD－A₁B₁C₁D₁的棱长为a，求异面直线A₁C₁与BD₁的距离．

Answer 1

答案：
解析：

解：连B1D1交A1C1于O，作OM⊥BD1于M． 　　∴A1C1⊥B1D1，BB1⊥A1C1，BB1∩B1D1＝B1． 　　∴A1C1⊥平面BB1D1．∴A1C1⊥OM，又OM⊥BD1． 　　∴OM是异面直线A1C1与BD1的公垂线． 　　在直角ΔBB1D1中作B1N⊥BD1于N． 　　∵BB1·B1D1＝B1N·BD1，a·a＝B1N·a， 　　∴B1N＝a，OM＝B1N＝a． 　　故异面直线A1C1与BD1的距离为a． 　　评析：作异面直线的公垂线一般是比较困难的，只有熟练地掌握线、线垂直，线、面垂直的关系后才能根据题目所给条件灵活作出．本题在求OM的长度时，主要运用中位线和面积的等量关系．

提示：

本题的关键是画出A1C1与BD1的公垂线，连B1D1交A1C1于O，在平面BB1D1内作OM⊥BD1，则OM就是A1C1与BD1的公垂线，问题得到解决．