题目内容
设函数 ,观察:
,观察: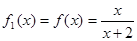 ,
,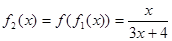 ,,
,, ,
, 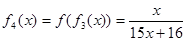 ……根据以上事实,由归纳推理可得当
……根据以上事实,由归纳推理可得当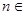 N*且
N*且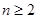 时,
时, 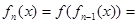 ( )
( )
A.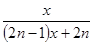 | B.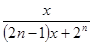 | C.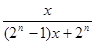 | D.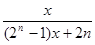 |
C
解析试题分析:观察所给的前四项的结构特点,先观察分子,只有一项组成,并且没有变化,在观察分母,有两部分组成,是一个一次函数,根据一次函数的一次项系数与常数项的变化特点,得到结果。根据观察: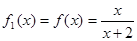 ,
,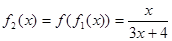 ,,
,, ,
, 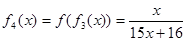 ,可知所给的函数式的分子不变都是x,而分母是由两部分的和组成,第一部分的系数分别是1,3,7,15…2n-1,第二部分的数分别是2,4,8,16…2n因此可知由归纳推理可得当
,可知所给的函数式的分子不变都是x,而分母是由两部分的和组成,第一部分的系数分别是1,3,7,15…2n-1,第二部分的数分别是2,4,8,16…2n因此可知由归纳推理可得当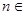 N*且
N*且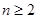 时,
时, 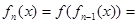
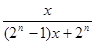 ,故选C.
,故选C.
考点:归纳推理
点评:本题考查归纳推理,实际上本题考查的重点是给出一个数列的前几项写出数列的通项公式,本题是一个综合题目,知识点结合的比较巧妙.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
设函数 若
若 是奇函数,则
是奇函数,则 的值是( )
的值是( )
A. | B.-4 | C. | D.4 |
已知函数f(x)=ex,对于曲线y=f(x)上横坐标成等差数列的三个点A,B,C,给出以下判断:
①△ABC一定是钝角三角形
②△ABC可能是直角三角形
③△ABC可能是等腰三角形
④△ABC不可能是等腰三角形
其中,正确的判断是
| A.①③ | B.①④ | C.②③ | D.②④ |
下列函数中,值域为 的是
的是
A. | B. | C. | D. |
如图,在平面直角坐标系中,正六边形 的中心在坐标原点,边长为
的中心在坐标原点,边长为 ,
, 平行于
平行于 轴,直线
轴,直线 (
( 为常数)与正六边形交于
为常数)与正六边形交于 两点,记
两点,记 的面积为
的面积为 ,则关于函数
,则关于函数 的奇偶性的判断正确的是( )
的奇偶性的判断正确的是( )
| A.一定是奇函数 | B.—定是偶函数 |
| C.既不是奇函数,也不是偶函数 | D.奇偶性与 有关 有关 |
函数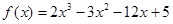 在
在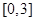 上的最大值和最小值分别是 ( )
上的最大值和最小值分别是 ( )
A.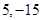 | B.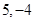 | C.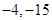 | D.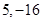 |
定义在R上的函数y=f(x)是增函数,且函数y=f(x-3)的图象关于点(3,0)成中心对称,若s,t满足f(s -2s) ≥-f(2t-t
-2s) ≥-f(2t-t ),则
),则
| A.s≥t | B.s<t | C.|s-1|≥|t-1| | D.s+t≥0 |
函数 在[0,3]上的最大值、最小值分别是( )
在[0,3]上的最大值、最小值分别是( )
| A.-4,-15 | B.5,-4 | C.5,-15 | D.5,-16 |
下列函数中,在其定义域内既是奇函数又是减函数的是( )
A. | B. | C. | D. |