题目内容
已知函数f(x)=log4(ax2+2x+3).
(1)若f(x)定义域为R,求a的取值范围;
(2)若f(1)=1,求f(x)的单调区间.
解析: (1)因为f(x)的定义域为R,
所以ax2+2x+3>0对任意x∈R恒成立,
显然a=0时不合题意,
从而必有 即
即 解得a>
解得a> .
.
即a的取值范围是 .
.
(2)∵f(1)=1,∴log4(a+5)=1,因此a+5=4,a=-1,这时f(x)=log4(-x2+2x+3).
由-x2+2x+3>0得-1<x<3,即函数定义域为(-1,3).
令g(x)=-x2+2x+3.
则g(x)在(-1, 1)上单调递增,在(1,3)上单调递减,
又y=log4x在(0,+∞)上单调递增,
所以f(x)的单调递增区间是(-1,1),
单调递减区间是(1,3).

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
 中,若
中,若 则此三角形一定是 ( )
则此三角形一定是 ( ) 的虚部是
的虚部是  ,则cos(15°-α)的值为( )
,则cos(15°-α)的值为( ) D.
D. 是定义在R上的可导函数,则下列说法不正确的是
是定义在R上的可导函数,则下列说法不正确的是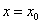 时取得极值,则
时取得极值,则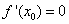
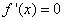 ,则
,则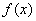 在
在