Question

    已知f (x) = xlnx.

    （I）求f (x) 在[t，t+2]（t>0）上的最小值；

    （Ⅱ）证明：都有。

Answer 1

    （Ⅰ）解：，令.

当单调递减；

当单调递增. …………………………………………（2分）

因为，

（1）当0＜t＜时；

（2）当t≥时，

所以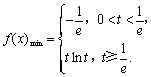  ………………………………………………………（6分）

（Ⅱ）证明：由（Ⅰ）知，当时，

的最小值是，（当且仅当x=时取到最小值）

问题等价于证明，

设，

则，易得，（当且仅当x=1时取到最大值）

从而对一切，都有成立.  ……………………………（12分）

请考生在22、23、24三题中任选一题作答，如果多做，则按所做第一题记分.