题目内容
已知曲线
（t为参数），
（θ为参数），点P，Q分别在曲线C1和C2上，求线段|PQ|长度的最小值．
解：C1：2x-y-10=0，Q到直线C1的距离
，
|PQ|≥=
≥
，
故所求的结果为
．
分析：把直线的参数方程化为普通方程，求出点到直线的距离 d 并化简为，利用正弦函数值域得其最小值．
点评：本题考查直线的参数方程，点到直线的距离公式及正弦函数值域的应用，化简d= 是解题的关键．
，|PQ|≥
=≥，故所求的结果为
．分析：把直线的参数方程化为普通方程，求出点到直线的距离 d 并化简为
，利用正弦函数值域得其最小值．点评：本题考查直线的参数方程，点到直线的距离公式及正弦函数值域的应用，化简d=
是解题的关键． 
练习册系列答案
名校课堂系列答案
相关题目
：
(t为参数)与曲线
：
(
为参数，
) 有一个公共点在X轴上，则
.
：
(t为参数)与曲线
：
(
为参数，
) 有一个公共点在X轴上，则
.
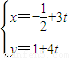（t为参数）与曲线
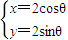（θ为参数）的交点为A，B，，则|AB|= ．
（t为参数），
，C
的方程为普通方程，并说明它们分别表示什么曲线；
，Q为C
中点
到直线
（t为参数）距离的最小值。
：
(t为参数)与曲线
：
(
为参数，
) 有一个公共点在X轴上，则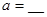
.