题目内容
如图，过抛物线y2=2px（p＞0）的焦点F的直线L交抛物线于点A、B，交其准线于点C，若|BC|=2|BF|，且|AF|=3，则此抛物线的方程为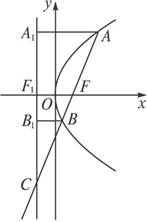
A.y2=
x B.y2=3x C.y2=
x D.y2=9x
B 过A、B分别作准线的垂线,垂足为A1、B1,记准线与x轴交点为F1,则BF=BB1,∵|CB|=2|BF|,∴|CB|=2|BB1|.
∴∠B1CB=30°.
∴|A1A|=|AC|.∵|AA1|=|AF|=3,∴|AC|=6.∴F为AC中点.∴|FF1|=|AA1|=
.
∴抛物线方程为y2=2×
x,即y2=3x.
练习册系列答案
名校课堂系列答案
相关题目
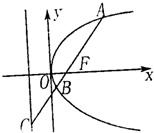如图，过抛物线y2=2px（p＞0）的焦点F的直线l交抛物线于点A、B，交其准线于点C，若|BC|=2|BF|，且|AF|=3，则此抛物线的方程为
78、如图，过抛物线y2=4x的焦点F的直线交抛物线与圆（x-1）2+y2=1于A，B，C，D四点，则|AB|•|CD|=
如图，过抛物线y2=2px（p＞0）的焦点F的直线l交抛物线于点A、B（|AF|＞|BF|），交其准线于点C，若|BC|=2|BF|，且|AF|=2，则此抛物线的方程为
如图，过抛物线y2=2px（p＞0）的焦点F且倾斜角为60°的直线l交抛物线于A、B两点，若|AF|=3，则此抛物线方程为（ ）
如图，过抛物线y2=4x焦点的直线依次交抛物线与圆（x-1）2+y2=1于A，B，C，D，则