题目内容
8.已知a、b、c分别是△ABC的三个内角A、B、C所对的边.(1)若a=ccosB,且b=csinA,试判断△ABC的形状;
(2)若△ABC的面积S△ABC=$\frac{\sqrt{3}}{2}$,c=2,A=60°,求a、b的值.
分析 (1)由a=ccosB,利用余弦定理可得a=c×$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$,解得a2+b2=c2,可得C=90°,由b=csinA,结合正弦定理可得A=B,即可得解三角形为等腰直角三角形.
(2)由S△ABC=$\frac{1}{2}$bcsinA=$\frac{\sqrt{3}}{2}$,解得b,由余弦定理即可解得a.
解答 解:(1)由a=ccosB,可得a=c×$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$,即a2+b2=c2,可得C=90°.
由b=csinA,结合正弦定理可得sinB=sinA,可得A=B,
所以三角形为等腰直角三角形;…6分
(2)由S△ABC=$\frac{1}{2}$bcsinA=$\frac{\sqrt{3}}{2}$,解得b=1,
由a2=c2+b2-2bccosA,解得a=$\sqrt{3}$.…12分
点评 本题主要考查了正弦定理,余弦定理,三角形面积公式的应用,熟练掌握相关公式及定理是解题的关键,属于中档题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
19.曲线y=$\frac{3x+4}{x+2}$在点(-1,1)处的切线方程为( )
| A. | y=2x+3 | B. | y=2x+1 | C. | y=-2x-1 | D. | y=-2x |
3.已知点A(2,-3),B(-3,-2)直线l过点P(1,1),且与线段AB相交,则直线l的斜率k的取值范围是( )
| A. | $(-∞,-4]∪[\frac{3}{4},+∞)$ | B. | $(-∞,-\frac{1}{4}]∪[\frac{3}{4},+∞)$ | C. | $[-4,\frac{3}{4}]$ | D. | $[\frac{3}{4},4]$ |
13.函数f(x)=(x-1)ln|x|的图象大致为( )
| A. | 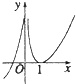 | B. | 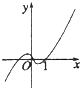 | C. | 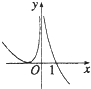 | D. | 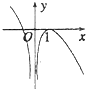 |