题目内容
 如图所示,圆O的两弦AB和CD交于点E,EF∥CB,EF交AD的延长线于点F,FG切圆O于点G.
如图所示,圆O的两弦AB和CD交于点E,EF∥CB,EF交AD的延长线于点F,FG切圆O于点G.(1)求证:△DFE∽△EFA;
(2)如果EF=1,求FG的长.
分析:(1)由同位角相等得出∠BCE=∠FED,由圆中同弧所对圆周角相等得出∠BAD=∠BCD,结合公共角∠EFD=∠EFD,证出△DEF∽△EFA;
(2)由(1)得EF2=FA•FD,再由圆的切线长定理FG2=FD•FA,所以FG=EF=1.
(2)由(1)得EF2=FA•FD,再由圆的切线长定理FG2=FD•FA,所以FG=EF=1.
解答: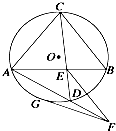 证明:(1)∵EF∥CB∴∠DEF=∠DCB.
证明:(1)∵EF∥CB∴∠DEF=∠DCB.
∴∠DEF=∠DAB,∴∠DEF=∠DAB.
又∵∠DFE=∠EFA∴△DFE∽△EFA…(4分)
(2)解∵△DFE∽△EFA,
∴
=
.∴EF2=FA•FD.
又∵FG切圆于G,
∴GF2=FA•FD.
∴EF2=FG2.∴EF=FG.
已知EF=1,
∴FG=1…(8分)
 证明:(1)∵EF∥CB∴∠DEF=∠DCB.
证明:(1)∵EF∥CB∴∠DEF=∠DCB.∴∠DEF=∠DAB,∴∠DEF=∠DAB.
又∵∠DFE=∠EFA∴△DFE∽△EFA…(4分)
(2)解∵△DFE∽△EFA,
∴
| EF |
| FA |
| FD |
| EF |
又∵FG切圆于G,
∴GF2=FA•FD.
∴EF2=FG2.∴EF=FG.
已知EF=1,
∴FG=1…(8分)
点评:本题考查与圆有关的角、比例线段,要善于寻找有关线段的数量关系,结合相关性质、定理求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
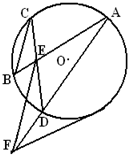 选修4-1:几何证明选讲
选修4-1:几何证明选讲

