题目内容
(本题满分10分)如图所示,圆O的两弦AB和CD交于点E,EF∥CB,EF交AD的延长线于点F,FG切圆O于点G.
(1)求证:△DFE∽△EFA;
(2)如果EF=1,求FG的长.

【答案】
(1)见解析;(2)见解析.
【解析】(1)在已有一个公共角∠DFE=∠EFA情况下,关键再证∠DEF=∠FAB即可.
(2) ∵△DFE∽△EFA,∴ =
= .∴EF2=FA·FD.
.∴EF2=FA·FD.
∵FG切圆于G,∴FG2=FA·FD.到此问题基本得到解决.
(1)证明 ∵EF∥CB,
∴∠DEF=∠DCB.
∵∠DCB=∠DAB,
∴∠DEF=∠DAB.
∵∠DFE=∠EFA,
∴△DFE∽△EFA.
(2)∵△DFE∽△EFA,∴ =
= .
.
∴EF2=FA·FD.
∵FG切圆于G,∴FG2=FA·FD.
∴EF2=FG2.∴EF=FG.∵EF=1,∴FG=1.

练习册系列答案
相关题目

 (假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动).
(假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动). 的概率?
的概率? ,求
,求


 -
- 中,
中, 分别是
分别是 ,
,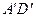 的中点,
的中点, 分别是
分别是 ,
,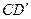 中点,
中点,

 的体积;
的体积;