题目内容
如图,已知某椭圆的焦点是F1(-4,0)、F2(4,0),过点F2并垂直于x轴的直线与椭圆的一个交点为B,且|F1B|+|F2B|=10,椭圆上不同的两点A(x1,y1),C(x2,y2)满足条件 |F2A|、|F2B|、|F2C|成等差数列(1)求该弦椭圆的方程;(2)求弦AC中点的横坐标;(3)设弦AC的垂直平分线的方程为y=kx+m,求m的取值范围 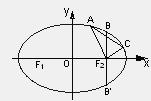

(1)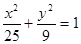 (2)
(2)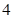 (3)-
(3)-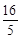 <m<
<m<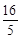
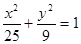 (2)
(2)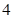 (3)-
(3)-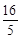 <m<
<m<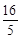
【错解分析】椭圆的定义、等差数列的定义,处理直线与圆锥曲线的方法
【正解】(1)由椭圆定义及条件知,2a=|F1B|+|F2B|=10,得a=5,又c=4,所以b=
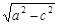 =3
=3 故椭圆方程为
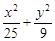 =1
=1 (2)由点B(4,yB)在椭圆上,得|F2B|=|yB|=
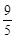 因为椭圆右准线方程为x=
因为椭圆右准线方程为x=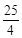 ,离心率为
,离心率为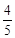 ,根据椭圆定义,有|F2A|=
,根据椭圆定义,有|F2A|=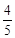 (
(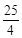 -x1),|F2C|=
-x1),|F2C|=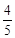 (
(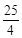 -x2),由|F2A|、|F2B|、|F2C|成等差数列,得
-x2),由|F2A|、|F2B|、|F2C|成等差数列,得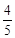 (
(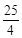 -x1)+
-x1)+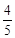 (
(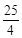 -x2)=2×
-x2)=2×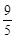 ,由此得出 x1+x2=8 设弦AC的中点为P(x0,y0),则x0=
,由此得出 x1+x2=8 设弦AC的中点为P(x0,y0),则x0=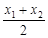 =4
=4 (3)解法一 由A(x1,y1),C(x2,y2)在椭圆上 得
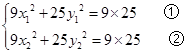
①-②得9(x12-x22)+25(y12-y22)=0,即9×
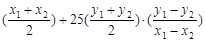 =0(x1≠x2)
=0(x1≠x2)将
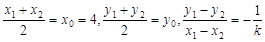 (k≠0)代入上式,得9×4+25y0(-
(k≠0)代入上式,得9×4+25y0(-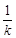 )=0 (k≠0)
)=0 (k≠0)即k=
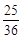 y0(当k=0时也成立) 由点P(4,y0)在弦AC的垂直平分线上,得y0=4k+m,
y0(当k=0时也成立) 由点P(4,y0)在弦AC的垂直平分线上,得y0=4k+m,所以m=y0-4k=y0-
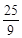 y0=-
y0=-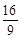 y0 由点P(4,y0)在线段BB′(B′与B关于x轴对称)的内部,
y0 由点P(4,y0)在线段BB′(B′与B关于x轴对称)的内部,得-
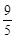 <y0<
<y0<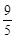 ,所以-
,所以-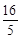 <m<
<m<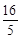
解法二 因为弦AC的中点为P(4,y0),所以直线AC的方程为
y-y0=-
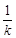 (x-4)(k≠0)③将③代入椭圆方程
(x-4)(k≠0)③将③代入椭圆方程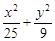 =1,得(9k2+25)x2-50(ky0+4)x+25(ky0+4)2-25×9k2=0所以x1+x2=
=1,得(9k2+25)x2-50(ky0+4)x+25(ky0+4)2-25×9k2=0所以x1+x2=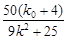 =8,解得k=
=8,解得k=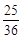 y0 (当k=0时也成立)
y0 (当k=0时也成立)
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
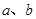 是非零实数,则方程
是非零实数,则方程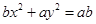 及
及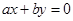 所表示的图形可能是( )
所表示的图形可能是( )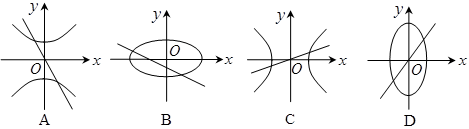
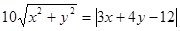 ,则动点M的轨迹方程是
,则动点M的轨迹方程是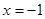 相切。记动点P的轨迹为C。
相切。记动点P的轨迹为C。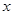 轴上,一条经过点
轴上,一条经过点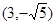 且倾斜角余弦值为
且倾斜角余弦值为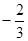 的直线
的直线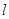 交椭圆于A,B两点,交
交椭圆于A,B两点,交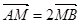 .
.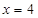 ,右焦点
,右焦点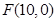 ,离心率
,离心率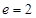 ,求双曲线方程.
,求双曲线方程.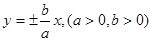 ,若双曲线上有一点M(
,若双曲线上有一点M(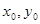 ),使
),使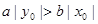 ,那双曲线的交点( )。
,那双曲线的交点( )。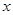 轴上
轴上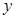 轴上
轴上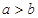 时在
时在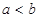 时在
时在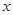 轴上的椭圆
轴上的椭圆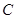 过点
过点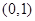 ,且离心率为
,且离心率为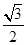 ,
,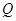 为椭圆
为椭圆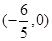 的直线
的直线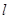 与椭圆
与椭圆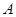 ,
,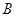 两点.
两点.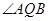 的大小;
的大小;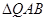 为等腰三角形?如果存在,求出直线
为等腰三角形?如果存在,求出直线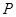 是椭圆
是椭圆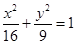 上的点,
上的点, 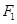 、
、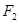 是椭圆的两个焦点,则
是椭圆的两个焦点,则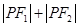 的值为
的值为