题目内容
以边长为 的正三角形作为底面的斜三棱柱,它的一条侧棱AA1与相邻两边都成450角,若此斜三棱柱的侧面积为
的正三角形作为底面的斜三棱柱,它的一条侧棱AA1与相邻两边都成450角,若此斜三棱柱的侧面积为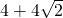 ,则棱柱的侧棱长为________.
,则棱柱的侧棱长为________.
2
分析:根据题意画出斜三棱柱,作出已知的线线角,根据线面垂直的判定定理证明BC⊥B1B,再由测面积的值列出关于侧棱的方程,然后求出侧棱的值.
解答:过A1做AA1的垂线A1D,取BC的中点E,连接AE,
由题意知A1在底面上的射影在线段AE上,
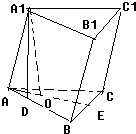
∵△ABC是正三角形,∴AE⊥BC,
根据线面垂直的判定定理知,BC⊥平面A1AE
∴BC⊥AA1,BC⊥BB1,
∵AB⊥DA1,∴∠DAA1=450,设棱AA1=a,则DA1= ,
,
∵斜三棱柱的侧面积为4+4 ,
,
∴4+4 =2×
=2× ×
× +
+ a,
a,
解得,a=2 ,
,
故答案为:2 .
.
点评:本题考查了棱柱的侧面积问题,需要画出几何体,根据线面垂直的定理进行证明侧面的高线,再由平行四边形的面积公式表示出侧面积,列出对应方程进行求解,难度较大,考查了空间想象能力.

分析:根据题意画出斜三棱柱,作出已知的线线角,根据线面垂直的判定定理证明BC⊥B1B,再由测面积的值列出关于侧棱的方程,然后求出侧棱的值.
解答:过A1做AA1的垂线A1D,取BC的中点E,连接AE,
由题意知A1在底面上的射影在线段AE上,

∵△ABC是正三角形,∴AE⊥BC,
根据线面垂直的判定定理知,BC⊥平面A1AE
∴BC⊥AA1,BC⊥BB1,
∵AB⊥DA1,∴∠DAA1=450,设棱AA1=a,则DA1=
 ,
,∵斜三棱柱的侧面积为4+4
 ,
,∴4+4
 =2×
=2× ×
× +
+ a,
a,解得,a=2
 ,
,故答案为:2
 .
.点评:本题考查了棱柱的侧面积问题,需要画出几何体,根据线面垂直的定理进行证明侧面的高线,再由平行四边形的面积公式表示出侧面积,列出对应方程进行求解,难度较大,考查了空间想象能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 (2009•南汇区二模)如图,将一个边长为1的正三角形的每条边三等分,以中间一段为边向形外作正三角形,并擦去中间一段,得图(2),如此继续下去,得图(3)…试用 n表示出第n个图形的边数an=
(2009•南汇区二模)如图,将一个边长为1的正三角形的每条边三等分,以中间一段为边向形外作正三角形,并擦去中间一段,得图(2),如此继续下去,得图(3)…试用 n表示出第n个图形的边数an= 上,以M为圆心的圆与x轴相切于椭圆的右焦点,若圆M与y轴相交于A,B两点,且△ABM是边长为
上,以M为圆心的圆与x轴相切于椭圆的右焦点,若圆M与y轴相交于A,B两点,且△ABM是边长为 的正三角形,
的正三角形, ,求直线l的斜率;
,求直线l的斜率;  左半部分交于H,K两点,又过椭圆N的右焦点F1做平行于HK的直线交椭圆N于R,S两点,试判断满足
左半部分交于H,K两点,又过椭圆N的右焦点F1做平行于HK的直线交椭圆N于R,S两点,试判断满足 的直线GK是否存在?请说明理由。
的直线GK是否存在?请说明理由。 =1(a>b>0)上,以M为圆心的圆与x轴相切于椭圆的右焦点,若圆M与y轴相交于A,B两点,且△ABM是边长为
=1(a>b>0)上,以M为圆心的圆与x轴相切于椭圆的右焦点,若圆M与y轴相交于A,B两点,且△ABM是边长为 的正三角形.
的正三角形.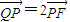 ,求直线l的斜率;
,求直线l的斜率; 左半部分交于H,K两点,又过椭圆N的右焦点F1做平行于HK的直线交椭圆N于R,S两点,试判断满足|GH|•|GK|=3|RF1|•|F1S|的直线GK是否存在?请说明理由.
左半部分交于H,K两点,又过椭圆N的右焦点F1做平行于HK的直线交椭圆N于R,S两点,试判断满足|GH|•|GK|=3|RF1|•|F1S|的直线GK是否存在?请说明理由.