题目内容
(文科)设直线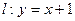 与椭圆
与椭圆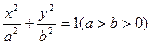 相交于A、B两个不
相交于A、B两个不
同的点,与x轴相交于点F.
(I)证明: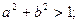
(II)若F是椭圆的一个焦点,且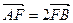 ,求椭圆的方程。
,求椭圆的方程。
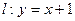 与椭圆
与椭圆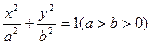 相交于A、B两个不
相交于A、B两个不同的点,与x轴相交于点F.
(I)证明:
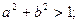
(II)若F是椭圆的一个焦点,且
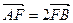 ,求椭圆的方程。
,求椭圆的方程。(1)略
(2)

(文科)(Ⅰ)证明:将 ,消去x,得
,消去x,得
 ① ……………………3分
① ……………………3分
由直线l与椭圆相交于两个不同的点,得
 ,所以
,所以 …….5分
…….5分
(Ⅱ)解:设 由①,
由①,
得 …7分
…7分
因为 所以,
所以,
 消去y2,
消去y2,
得 ,化简,得
,化简,得 ……… 9分
……… 9分
若F是椭圆的一个焦点,则c=1,b2=a2-1 代入上式,
解得 ………………11分
………………11分
所以,椭圆的方程为 ………………13分
………………13分
 ,消去x,得
,消去x,得 ① ……………………3分
① ……………………3分由直线l与椭圆相交于两个不同的点,得
 ,所以
,所以 …….5分
…….5分(Ⅱ)解:设
 由①,
由①,得
 …7分
…7分因为
 所以,
所以, 消去y2,
消去y2,得
 ,化简,得
,化简,得 ……… 9分
……… 9分若F是椭圆的一个焦点,则c=1,b2=a2-1 代入上式,
解得
 ………………11分
………………11分所以,椭圆的方程为
 ………………13分
………………13分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
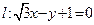 ,求
,求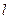 关于
关于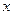 轴对称的直线方程;
轴对称的直线方程;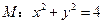 ,求过点
,求过点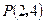 与圆
与圆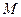 相切的切线方程
相切的切线方程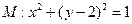 ,
,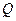 是
是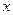 轴上的动点,
轴上的动点,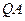 、
、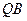 分别切圆
分别切圆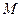 于
于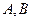 两点
两点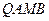 的面积的最小值
的面积的最小值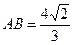 ,求直线
,求直线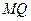 的方程
的方程 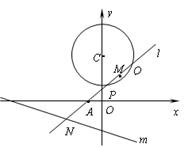
 的动直线
的动直线 与圆
与圆 :
: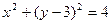 相交于
相交于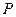 、
、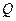 两点,
两点,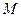 是
是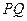 中点,
中点,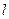 与直线
与直线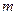 :
: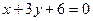 相交于
相交于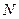 .
.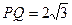 时,求直线
时,求直线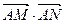 是否与直线
是否与直线 与圆
与圆 交于
交于 两点,且
两点,且 对称,
对称, 的值;
的值; 与
与 交
交 两点,是否存在实数
两点,是否存在实数 使得
使得 ,如果存在,求出
,如果存在,求出 且与直线
且与直线 相切的圆的方程是_______________.
相切的圆的方程是_______________. 沿
沿 轴向左平移1个单位,所得直线与圆
轴向左平移1个单位,所得直线与圆 相切,则实数
相切,则实数 的值为 ( )
的值为 ( )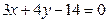 与圆
与圆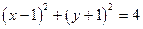 的位置关系是( )
的位置关系是( )