题目内容
已知点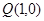 在椭圆C:
在椭圆C: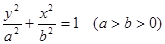 上,且椭圆C的离心率为
上,且椭圆C的离心率为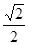 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点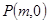 作直线交椭圆C于点
作直线交椭圆C于点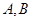 ,
, 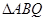 的垂心为
的垂心为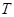 ,是否存在实数
,是否存在实数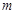 ,使得垂心
,使得垂心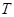 在Y轴上.若存在,求出实数
在Y轴上.若存在,求出实数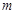 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
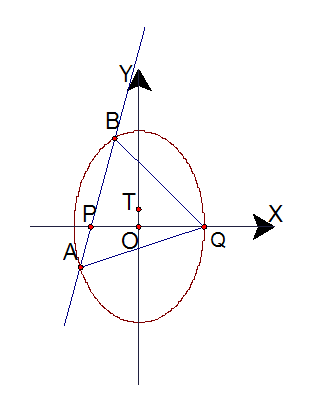
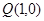 在椭圆C:
在椭圆C: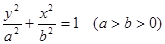 上,且椭圆C的离心率为
上,且椭圆C的离心率为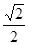 .
.(Ⅰ)求椭圆C的方程;
(Ⅱ)过点
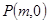 作直线交椭圆C于点
作直线交椭圆C于点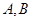 ,
, 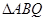 的垂心为
的垂心为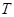 ,是否存在实数
,是否存在实数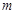 ,使得垂心
,使得垂心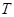 在Y轴上.若存在,求出实数
在Y轴上.若存在,求出实数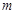 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
21.解:(Ⅰ)  ,
,
 ,
,

 椭圆C的方程为
椭圆C的方程为 ——————————————3分
——————————————3分
(Ⅱ)假设存在实数m,使得垂心T在Y轴上。
当直线斜率不存在时,设 ,则
,则
则有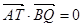 ,所以
,所以
又
可解得
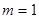 (舍)
(舍)
 ——————————————5分
——————————————5分
当直线斜率存在时,设 (
( )
) ,
,
设直线方程为:
则 斜率为
斜率为 ,
, ,
,
又 ,
,

即:


 ————————————7分
————————————7分
 消去
消去 可得:
可得:




 =
=
————————————10分
代入可得( )
)





又

综上知实数m的取值范围 ——————————12分
——————————12分
(其它解法酌情给分)
 ,
,
 ,
,

 椭圆C的方程为
椭圆C的方程为 ——————————————3分
——————————————3分(Ⅱ)假设存在实数m,使得垂心T在Y轴上。
当直线斜率不存在时,设
 ,则
,则
则有
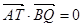 ,所以
,所以
又

可解得

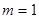 (舍)
(舍) ——————————————5分
——————————————5分当直线斜率存在时,设
 (
( )
) ,
,
设直线方程为:

则
 斜率为
斜率为 ,
, ,
,
又
 ,
,

即:



 ————————————7分
————————————7分 消去
消去 可得:
可得:




 =
=
————————————10分
代入可得(
 )
)




又


综上知实数m的取值范围
 ——————————12分
——————————12分(其它解法酌情给分)
略

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
 的共同焦点为
的共同焦点为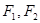 ,
,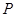 是两曲线的一个交点,则
是两曲线的一个交点,则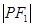 ·
· 的值为______________.
的值为______________.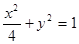 的长轴长等于 ▲ .
的长轴长等于 ▲ .
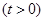 在直线
在直线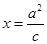 (
(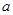 为长半轴,
为长半轴,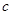 为半焦距)上.
为半焦距)上.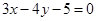 截得的弦长为2的圆的方程;
截得的弦长为2的圆的方程;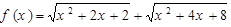 的最小值为( )
的最小值为( )



 及以下3个函数:①
及以下3个函数:①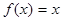 ;②
;②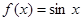 ;
;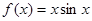 ,其中函数图像能等分该椭圆面积的函数个数有……………( ).
,其中函数图像能等分该椭圆面积的函数个数有……………( ).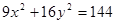 内有一点P
内有一点P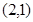 ,以P为中点作弦MN,则直线MN的方程是( )
,以P为中点作弦MN,则直线MN的方程是( )



 的离心率为
的离心率为 ,则
,则 的值为_____________.
的值为_____________. ,且长轴长是短轴长的2倍,则该椭圆的标准方程是________.
,且长轴长是短轴长的2倍,则该椭圆的标准方程是________.