Question

【题目】某个部件由三个元件按图方式连接而成，元件1或元件2正常工作，且元件3正常工作，则部件正常工作（其中元件1，2，3正常工作的概率都为 ），设三个电子元件的使用寿命（单位：小时）均服从正态分布N（1000，502），且各个元件能否正常工作相互独立，那么该部件的使用寿命超过1000小时的概率为（ ）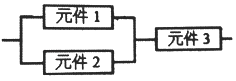
A.
B.
C.
D.

Answer 1

【答案】D
【解析】解：∵三个电子元件的使用寿命均服从正态分布N（1000，502）， ∴三个电子元件的使用寿命超过1000小时的概率为p= ，
设A={超过1000小时时，元件1、元件2至少有一个正常}，
B={超过1000小时时，元件3正常}，
C={该部件的使用寿命超过1000小时}，
则P（A）=1﹣（1﹣ ）2= ，P（B）= ，
故该部件的使用寿命超过1000小时的概率P（C）=P（AB）=P（A）P（B）= = ．
故选：D．