题目内容
已知函数
．
（1）求证：函数f（x）在（﹣∞，0]上是增函数．
（2）求函数
在[﹣3，2]上的最大值与最小值．
．（1）求证：函数f（x）在（﹣∞，0]上是增函数．
（2）求函数
在[﹣3，2]上的最大值与最小值．（1）证明：设x1＜x2＜0，则
因x1＜x2＜0，有x1+x2＜0，x2﹣x1＞0，
又（1+x12）（1+x22）＞0
所以
，得f（x1）﹣f（x2）＜0
故f（x）为（﹣∞，0]上的增函数．
（2）解：因为函数f（x）定义域为R，且f（﹣x）=f（x），所以函数f（x）为偶函数
又f（x）在（﹣∞，0]上为增函数，
所以f（x）在[0，+∞）上为减函数
所以函数的最大值为f（0）=1．
又当x=﹣3时，
，
当x=2时，
，
故函数的最小值为
．
练习册系列答案
阅读快车系列答案
相关题目
．
；
．
；
.
．
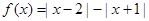在区间
上存在唯一的极值点，并用二分法求函数取得极值时相应
的近似值（误差不超过
）；（参考数据
，
，
）
时，若关于
恒成立，试求实数
的取值范围.
．
在区间
上存在唯一的极值点，并用二分法求函数取得极值时相应
的近似值（误差不超过
）；（参考数据
，
，
）
时，若关于
恒成立，试求实数
的取值范围.