题目内容
已知A、B、C是最大边长为2的△ABC的三个内角,
=(2sin
,4sin
),|
|=
.
(1)求tanA•tanB的值.(2)求∠C的最大值及此时△ABC的面积.
| m |
| A-B |
| 2 |
| C |
| 2 |
| m |
| 10 |
(1)求tanA•tanB的值.(2)求∠C的最大值及此时△ABC的面积.
(1)∵
2=4sin2
+16sin2
=10-2cos(A-B)+8cos(A+B)
=10-2cosAcosB-10sinAsinB=10∴tanAtanB=
(2)∴tanAtanB=
>0∴tanA>0,tanB>0
∴tanC=tan(A+B)=-
=-
(tanA+tanB)≤-
当且仅当tanA=tanB=
取等号.
又∠C>
,∴c为最大边.即c=2
由余弦定理:c2=a2+b2-2abcosC∴4=2a2-2a2×(-
)∴a2=
故S△=
absinC=
×
×
=
| m |
| A-B |
| 2 |
| C |
| 2 |
=10-2cosAcosB-10sinAsinB=10∴tanAtanB=
| 3 |
| 5 |
(2)∴tanAtanB=
| 3 |
| 5 |
∴tanC=tan(A+B)=-
| tanA+tanB |
| 1+tanAtanB |
| 5 |
| 2 |
| 15 |
当且仅当tanA=tanB=
| ||
| 5 |
又∠C>
| π |
| 2 |
由余弦定理:c2=a2+b2-2abcosC∴4=2a2-2a2×(-
| 1 |
| 4 |
| 8 |
| 5 |
故S△=
| 1 |
| 2 |
| 1 |
| 2 |
| 8 |
| 5 |
| ||
| 4 |
| ||
| 5 |

练习册系列答案
相关题目
 .
.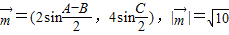 .
.