题目内容
6.直线l过点P(3,-1),点A(-1,-2)到l的距离为4,此时直线l的方程为x=3或17x-8y-59=0.分析 当直线l的斜率不存在时,直线l为x=3,A(-1,-2)到x=3的距离为4,成立;当直线l的斜率存在时,设直线l的方程为kx-y-3k-1=0,由点A(-1,-2)到l的距离为4,利用点到直线的距离公式求出k,由此能求出直线l的方程.
解答 解:∵直线l过点P(3,-1),
∴当直线l的斜率不存在时,直线l为x=3,A(-1,-2)到x=3的距离为4,成立;
当直线l的斜率存在时,设直线l的方程为y+1=k(x-3),即kx-y-3k-1=0,
∵点A(-1,-2)到l的距离为4,
∴$\frac{|-k+2-3k-1|}{\sqrt{{k}^{2}+1}}$=4,解得k=$\frac{17}{8}$,
∴直线l的方程为:$\frac{17}{8}x-y-3×\frac{17}{8}-1=0$,整理得17x-8y-59=0.
∴直线l的方程为x=3或17x-8y-59=0.
故答案为:x=3或17x-8y-59=0.
点评 本题考查直线方程的求法,是基础题,解题时要认真审题,注意点到直线的距离公式的合理运用.

练习册系列答案
相关题目
15.已知数列{an}的前n项和为Sn,且an≠0,则“Sn+1=3an+1+2Sn”是“数列{an}为等比数列”的( )
| A. | 充要条件 | B. | 充要不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
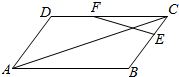 如图,在?ABCD中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,$\overrightarrow{CE}$=$\frac{1}{3}$$\overrightarrow{CB}$,$\overrightarrow{CF}$=$\frac{2}{3}$$\overrightarrow{CD}$.
如图,在?ABCD中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,$\overrightarrow{CE}$=$\frac{1}{3}$$\overrightarrow{CB}$,$\overrightarrow{CF}$=$\frac{2}{3}$$\overrightarrow{CD}$.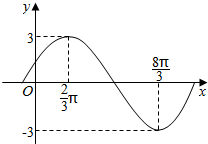 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,f(x)=3sin($\frac{1}{2}$x+$\frac{π}{6}$).
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,f(x)=3sin($\frac{1}{2}$x+$\frac{π}{6}$).