题目内容
【题目】在 
中， 
， 
， 
分别为角 
， 
， 
所对的边， 
为 的面积，且 
．
（I）求角 的大小；
（II）若 
， 
， 
为 
的中点，且 
，求 
的值．
【答案】解：（I）由已知得 
，
∴ 
.
即 
.
∴ 
.
又∵ 
， 
，
（II）由 
得：
，又∵ 
为 
的中点，∴ 
， 
，
∴ 
，即 
.
又∵ 
，
∴ 
.
又∵ 
，∴ 
， 
，
∴ 
【解析】(1)由题中已知的三角形面积公式，利用同角三角函数的基本关系式可求得tan A的值，再结合角A的范围即可求出A的值。(2)由D为BC的中点可得出DB=DC、AD的值，利用cos ∠ A D B = cos ∠ A D C结合余弦定理
整理可得 b2 + c2= 20，由(1)的结论结合余弦定理 可求出 b c的值，联立两式可分别别求出b、c的值，再利用正弦定理即可解得sinc的结果。
【考点精析】本题主要考查了余弦定理的定义的相关知识点，需要掌握余弦定理:
;
;
才能正确解答此题．
练习册系列答案
金钥匙试卷系列答案
相关题目
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程记录的产量 
（吨）与相应的生产能耗 
（吨标准煤）的几组对照数据：
| 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 |
参考公式：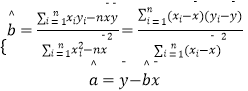 
（1）已知产量 和能耗 呈线性关系，请根据上表提供的数据，用最小二乘法求出 关于 的线性回归方程 
；
（2）已知该厂技改前100吨甲产品的生产耗能为90吨标准煤，试根据（1）求出的线性回归方程，预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤？
