题目内容
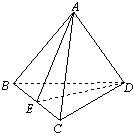
已知：空间四边形ABCD（如图所示），E、F分别是AB、AD的中点，G、H分别是BC、CD上的点.且CG=
BC，CH=
DC.求证： 
（1）E、F、G、H四点共面；
（2）三直线FH、EG、AC共点.
证明：（1）EFBD,GH
BD.
∴EF∥GH故EF与GH共面，即E、F、G、H四点共面.
（2）EF∥GH，但EF≠GH.
故EFGH是一个梯形.
设FH与EG交于O点则OEFH
面DAC，
O∈EG
面BAC.
∴O∈面DAC∩面BAC=AC.
即直线AC过O点，故三直线FH、EG、AC共点.
练习册系列答案
芝麻开花课程新体验系列答案
相关题目
已知在空间四边形ABCD中，E、F分别是AB、AD的中点，G、H分别是BC、CD上的点，且BG：GC=DH：HC=2：1，则EG、FH、AC的位置关系是（ ）| A、两两异面 | B、两两平行 | C、交于一点 | D、两两相交 |
已知：空间四边形ABCD，AB=AC，DB=DC，
（2011•顺义区一模）如图，已知在空间四边形ABCD中，AB=AC=DB=DC，E为BC的中点．