题目内容
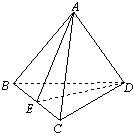已知：空间四边形ABCD，AB=AC，DB=DC，求证：BC⊥AD．
分析：利用等腰三角形的底边中线性质得到AE⊥BC，DE⊥BC，从而 BC⊥面ADE．
解答：解：取BC的中点为E，
∵AB=AC，∴AE⊥BC．
∵DB=DC，∴DE⊥BC．
这样，BC就和平面ADE内的两条相交直线AE、DE 垂直，
∴BC⊥面ADE，
∴BC⊥AD．
∵AB=AC，∴AE⊥BC．
∵DB=DC，∴DE⊥BC．
这样，BC就和平面ADE内的两条相交直线AE、DE 垂直，
∴BC⊥面ADE，
∴BC⊥AD．
点评：本题考查等腰三角形的底边中线性质，线面垂直的判定和性质．
练习册系列答案
综合自测系列答案
相关题目
已知在空间四边形ABCD中，E、F分别是AB、AD的中点，G、H分别是BC、CD上的点，且BG：GC=DH：HC=2：1，则EG、FH、AC的位置关系是（ ）| A、两两异面 | B、两两平行 | C、交于一点 | D、两两相交 |
（2011•顺义区一模）如图，已知在空间四边形ABCD中，AB=AC=DB=DC，E为BC的中点．