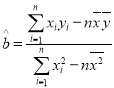题目内容
【题目】2019年,中国的国内生产总值(GDP)已经达到100亿元人民币,位居世界第二,这其中实体经济的贡献功不可没,实体经济组织一般按照市场化原则运行,某生产企业一种产品的成本由原料成本及非原料成本组成,每件产品的非原料成本![]() (元)与生产该产品的数量
(元)与生产该产品的数量![]() (千件)有关,经统计得到如下数据:
(千件)有关,经统计得到如下数据:

根据以上数据绘制了如下的散点图
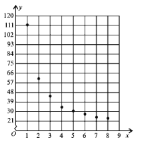
现考虑用反比例函数模型![]() 和指数函数模型
和指数函数模型![]() 分别对两个变量关系进行拟合,为此变换如下:令
分别对两个变量关系进行拟合,为此变换如下:令![]() ,则
,则![]() ,即
,即![]() 与
与![]() 也满足线性关系,令
也满足线性关系,令![]() ,则
,则![]() ,即
,即![]() 也满足线线关系,这样就可以使用最小二乘法求得非线性回归方程,已求得用指数函数模型拟合的回归方程为
也满足线线关系,这样就可以使用最小二乘法求得非线性回归方程,已求得用指数函数模型拟合的回归方程为![]() 与
与![]() 的相关系数
的相关系数![]() ,其他参考数据如下(其中
,其他参考数据如下(其中![]() )
)

(1)求指数函数模型和反比例函数模型中![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)试计算![]() 与
与![]() 的相关系数
的相关系数![]() ,并用相关系数判断:选择反比例函数和指数函数两个模型中哪一个拟合效果更好(精确到0.01)?
,并用相关系数判断:选择反比例函数和指数函数两个模型中哪一个拟合效果更好(精确到0.01)?
(3)根据(2)小题的选择结果,该企业采用订单生产模式(即根据订单数量进行生产,产品全部售出),根据市场调研数据,该产品定价为100元时得到签到订单的情况如下表:
订单数(千件) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
概率 |
|
|
|
|
|
|
|
|
|
|
|
已知每件产品的原来成本为10元,试估算企业的利润是多少?(精确到1千元)
参考公式:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别是:
的斜率和截距的最小二乘估计分别是: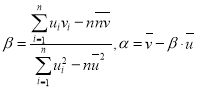 相关系数:
相关系数: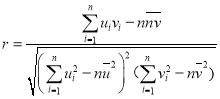
【答案】(1)指数模型回归方程为![]() ,反比例函数回归方程为
,反比例函数回归方程为![]() ;(2)反比例函数;(3)612(千元)
;(2)反比例函数;(3)612(千元)
【解析】
(1)对![]() 两边取对数,可得
两边取对数,可得![]() ,即
,即![]() ,再把
,再把![]() 代入,可求得
代入,可求得![]() ,然后令
,然后令![]() ,则
,则![]() ,结合参考公式即可求得
,结合参考公式即可求得![]() ,
,![]() ,从而求得回归方程;
,从而求得回归方程;
(2)利用参考公式求出相关系数![]() ,再与(1)中的
,再与(1)中的![]() 相比较,即可得解;
相比较,即可得解;
(3)设该企业的订单期望为![]() (千件),先利用错位相减法求出
(千件),先利用错位相减法求出![]() 的值,再算出企业的利润.
的值,再算出企业的利润.
解:(1)因为![]() ,所以
,所以![]() ,
,![]() ,将
,将![]() 代入上式,得
代入上式,得![]() ,所以
,所以![]() .
.
令![]() ,则
,则![]() ,因为
,因为![]() ,所以
,所以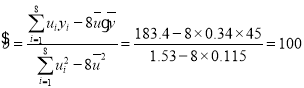 ,
,
则![]() ,
,
所以![]() , 所以y关于x的回归方程为
, 所以y关于x的回归方程为![]() .
.
综上,指数模型回归方程为![]() ,反比例函数回归方程为
,反比例函数回归方程为![]() ;
;
(2)y与![]() 的相关系数为
的相关系数为 ,
,
因为![]() ,所以用反比例函数模型拟合效果更好.
,所以用反比例函数模型拟合效果更好.
(3)设该企业的订单期望为S(千件),
则![]()
令![]() ①
①
![]() ②
②
②-①,得![]()
化简得![]() ,所以
,所以![]()
所以该企业的利润约为: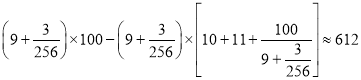 (千元)
(千元)

【题目】新能源汽车正以迅猛的势头发展,越来越多的企业不断推出纯电动产品,某汽车集团要对过去一年推出的四款纯电动车型中销量较低的![]() 车型进行产品更新换代.为了了解这种车型的外观设计是否需要改进,该集团委托某调查机构对大众做问卷调查,并从参与调查的人群中抽取了
车型进行产品更新换代.为了了解这种车型的外观设计是否需要改进,该集团委托某调查机构对大众做问卷调查,并从参与调查的人群中抽取了![]() 人进行抽样分析,得到如下表格:(单位:人)
人进行抽样分析,得到如下表格:(单位:人)
喜欢 | 不喜欢 | 合计 | |
青年人 |
|
|
|
中年人 |
|
|
|
合计 |
|
|
|
(1)根据表中数据,能否在犯错误的概率不超过![]() 的前提下认为大众对
的前提下认为大众对![]() 型车外观设计的喜欢与年龄有关?
型车外观设计的喜欢与年龄有关?
(2)现从所抽取的中年人中按是否喜欢![]() 型车外观设计利用分层抽样的方法抽取
型车外观设计利用分层抽样的方法抽取![]() 人,再从这
人,再从这![]() 人中随机选出
人中随机选出![]() 人赠送五折优惠券,求选出的
人赠送五折优惠券,求选出的![]() 人中至少有
人中至少有![]() 人喜欢该集团
人喜欢该集团![]() 型车外观设计的概率;
型车外观设计的概率;
(3)将频率视为概率,从所有参与调查的人群中随机抽取![]() 人赠送礼品,记其中喜欢
人赠送礼品,记其中喜欢![]() 型车外观设计的人数为
型车外观设计的人数为![]() ,求
,求![]() 的数学期望和方差.
的数学期望和方差.
参考公式: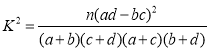 ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
【题目】下表是某公司![]() 年
年![]() 月份研发费用
月份研发费用![]() (百万元)和产品销量
(百万元)和产品销量![]() (万台)的具体数据:
(万台)的具体数据:
月 份 |
|
|
|
|
|
|
|
|
研发费用(百万元) |
|
|
|
|
|
|
|
|
产品销量(万台) |
|
|
|
|
|
|
|
|
(1)根据数据可知![]() 与
与![]() 之间存在线性相关关系,用线性相关系数说明
之间存在线性相关关系,用线性相关系数说明![]() 与
与![]() 之间的相关性强弱程度
之间的相关性强弱程度
(2)求出![]() 与
与![]() 的线性回归方程(系数精确到
的线性回归方程(系数精确到![]() ),并估计当研发费用为
),并估计当研发费用为![]() (百万元)时该产品的销量.
(百万元)时该产品的销量.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]()
参照公式:相关系数 ,其回归直线
,其回归直线![]() 中的
中的