题目内容
已知正四棱锥相邻两个侧面的夹角为120°,它的底面边长为a,求:(1)棱锥的高;
(2)斜高;
(3)侧棱长.

解析:过S作SO⊥底面AC于O,SG⊥BC于G,AE⊥SB于E,连结CE.
∵△SAB≌△SCB,
∴CE⊥SB.
∴∠AEC为侧面SAB与侧面SBC所成二面角的平面角.
∴∠AEC=120°.连结OE,
∵AO=CO,AE=CE,∴∠AEO=60°.
在Rt△AOE中,OE=![]() =
=![]() a,AE=
a,AE=![]() =
=![]() a,
a,
∴AE=CE=![]() a.∴BE=
a.∴BE=![]() =
=![]() a.
a.
∵∠CBE=∠SBG,∠SGB=∠CEB=90°,
∴Rt△SBG∽Rt△CBE.
∴SG=![]() ·CE=
·CE=![]() a.
a.
在Rt△SBG中,SB=![]() =
=![]() a.
a.
在Rt△SOG中,SO=![]() =
=![]() a.
a.
∴棱锥的高为![]() ,斜高为
,斜高为![]() a,侧棱长为
a,侧棱长为![]() a.
a.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
 ,则
,则 ;
;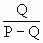 ;
;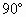 .
.