题目内容
已知函数
(1)函数f(x)的单调区间；
(2)设函数g(x)＝xf(x)＋t
(x)＋e－x(t∈R)，是否存在实数a，b，c∈[0，1]，使得g(a)＋g(b)＜g(c)？若存在，求出t的取值范围；若不存在，说明理由．
答案：
解析：
解析：
|
解：(1) 当 当 (2)假设存在 则 ∵ ∴ ①当 ∴ ②当 ∴ ③当 在 在 ∴ 即 由(1)知 故 而 ∴不等式(★)无解 16分 综上所述，存在 |
2分
时，
，
在区间
上为减函数
时，
，
在区间
上为增函数 4分
、
、
，使得
，
5分
7分
时，
，
在
上单调递减
即
，得
9分
时，
，
即
，得
11分
时，
，
，
在
上单调递减
，
，
在
上单调递增
(★) 13分
在
上单调递减
，使得命题成立．
练习册系列答案
相关题目
已知函数f（x）的导函数为f′（x）=2+cosx，x∈（-1，1），且f（0）=0，如果f（1-x）+f（1-x2）＜0，则实数x的取值范围为（ ）
| A、（0，1） | ||||
B、(1 ，
| ||||
C、(-2 ， -
| ||||
D、(1，
|
已知函数f（x）的定义域为[-2，+∞），部分对应值如表格所示，f′（x）为f（x）．的导函数，函数y=f′（x）的图象如右图所示：
已知函数f（x）=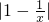
，x∈（0，+∞）．