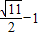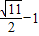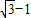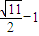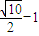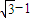Question

点M是抛物线y²=x上的动点，点N是圆C₁：（x+1）²+（y-4）²=1关于直线x-y+1=0对称的曲线C上的一点，则|MN|的最小值是（　　）

• A、

  11

  2

  -1
• B、

  10

  2

  -1
• C、2
• D、

  3

  -1

Answer 1

分析：由题意求出圆的对称圆的圆心坐标，求出对称圆的圆心坐标到抛物线上的坐标的距离的最小值，减去半径即可得到|MN|的最小值．

解答：解：圆C₁：（x+1）²+（y-4）²=1关于直线x-y+1=0对称的圆的圆心坐标（3，0），半径是1；
设M的坐标为（y²，y），所以圆心到M的距离：

(y2-3)2+ y2

，当y²=

5

2

时，它的最小值为

11

2

，
则|MN|的最小值是：

11

2

-1．
故选A．

点评：本题考查对称性问题，两点间的距离公式，函数最值的应用，考查计算能力，转化思想，好题．