题目内容
（本小题14分）已知点
，直线
，
为平面上的动点，过点作直线
的垂线，垂足为点
，且
.
（1）求动点的轨迹
的方程；
（2）轨迹上是否存在一点
使得过
的切线
与直线
平行？若存在，求出的方程，并求出它与
的距离；若不存在，请说明理由.
【答案】
19.解：（1）设点
，则
，
由
得 
整理得
…………………5分
（2）假设轨迹
上存在一点
使得过
的切线
与直线
平行.
由
得
，所以 
，
…………………7分
由假设可知，直线的斜率
…………………8分
又直线
的斜率等于1，故
， 即
，
…………………9分
代入
得 
…………………10分
因此点的坐标为
，直线的方程为
…………………12分
直线与直线的距离
. …………………14分
【解析】略
练习册系列答案
相关题目
点
，过
点作圆
的切线
为切点．
所在直线的方程；
；
的方程．
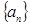满足
，且
是
，
的等差中项.
，
，求使 
成立的正整数
的最小值.
，设
。
图象上任意一点
为切点的切线的斜率
恒成立，求实数
的最小值。
，使得函数
的图象与
的图象恰好有四个不同的交点？若存在，求出
的图像与函数
的图像关于点
对称
，
在区间
上的值不小于6，求实数a的取值范围．
的图像在[a,b]上连续不断，定义：
，
，其中
表示函数
在D上的最小值，
表示函数
对任意的
成立，则称函数
上的“k阶收缩函数”
，试写出
，
的表达式；
试判断
，函数
是[0,b]上的2阶收缩函数，求b的取值范围