题目内容
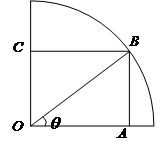
如图,半径为30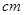 的圆形(
的圆形(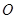 为圆心)铁皮上截取一块矩形材料
为圆心)铁皮上截取一块矩形材料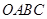 ,其中点
,其中点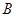 在圆弧上,点
在圆弧上,点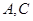 在两半径上,现将此矩形材料卷成一个以
在两半径上,现将此矩形材料卷成一个以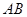 为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设
为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设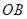 与矩形材料的边
与矩形材料的边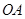 的夹角为
的夹角为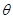 ,圆柱的体积为
,圆柱的体积为
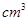 .
.
(Ⅰ)求 关于
关于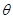 的函数关系式?
的函数关系式?
(Ⅱ)求圆柱形罐子体积 的最大值.
的最大值.
(Ⅰ)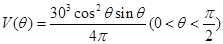 ;(Ⅱ)
;(Ⅱ)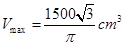 。
。
解析试题分析:方法一:(Ⅰ)在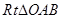 中,
中,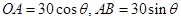 ,将此矩形材料卷成一个以
,将此矩形材料卷成一个以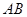 为母线的圆柱,则其底面周长为
为母线的圆柱,则其底面周长为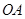 ,设地面半径为
,设地面半径为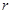 ,则
,则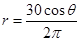 ,由柱体的体积公式,可知
,由柱体的体积公式,可知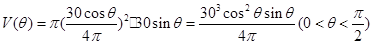 ;(Ⅱ)利用换元法求解,令
;(Ⅱ)利用换元法求解,令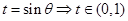 ,则
,则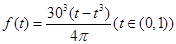 ,对其求导可知函数
,对其求导可知函数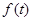 在
在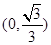 上单调递增,在
上单调递增,在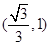 上单调递减,可知当
上单调递减,可知当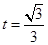 时,体积
时,体积 取得最大值
取得最大值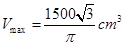 .
.
方法二:(1)连接OB,在Rt△OAB中,由AB=x,则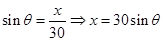 ,利用勾股定理可得
,利用勾股定理可得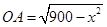 ,设圆柱底面半径为r,则
,设圆柱底面半径为r,则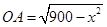 =2πr,即可得出r.
=2πr,即可得出r.
利用V=πr2•x(其中0<x<30)即可得出V与x的关系,进而得到 关于
关于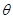 的函数关系式.
的函数关系式.
(2)利用(1)可知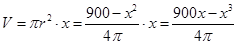 (
(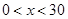 ),再对V求导得V′,得出其单调性,可知
),再对V求导得V′,得出其单调性,可知 在
在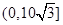 上是增函数,在
上是增函数,在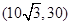 上是减函数,所以当
上是减函数,所以当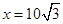 时,
时, 有最大值.
有最大值.
试题解析:【解法1】:(1)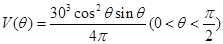
(2)令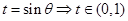 ,
,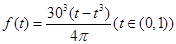 ,
,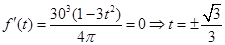
所以函数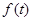 在
在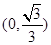 上单调递增,在
上单调递增,在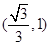 上单调递减,
上单调递减,
即当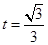 时,体积
时,体积 取得最大值
取得最大值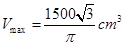 .
.
【解法2】:(1)连接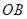 ,在
,在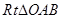 中,设
中,设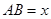 ,则
,则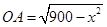
设圆柱底面半径为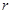 ,则
,则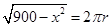 ,即
,即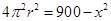 ,
,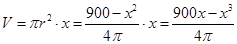 ,其中
,其中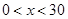 .
.
(2)由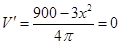 ,得
,得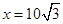 ;
;
由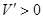 解得
解得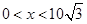 ;由
;由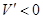 解得
解得 .
.
因此 在
在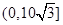 上是增函数,在
上是增函数,在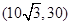 上是减函数.
上是减函数.
所以当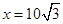 时,
时, 有最大值.
有最大值.
考点:1.导数在最大值、最小值问题中的应用;2.解三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (a为常数).
(a为常数).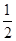 ,求证:当x∈(0,+∞)时,f(x)>1;
,求证:当x∈(0,+∞)时,f(x)>1; <e4(n∈N*)..
<e4(n∈N*)..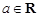 ,函数
,函数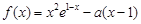 .
.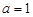 时,求
时,求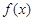 在
在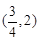 内的极大值;
内的极大值;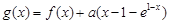 ,当
,当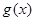 有两个极值点
有两个极值点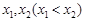 时,总有
时,总有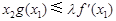 ,求实数
,求实数 的值.(其中
的值.(其中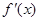 是
是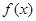 的导函数.)
的导函数.)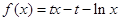
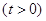 .
. 在
在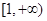 上为增函数,求实数
上为增函数,求实数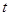 的取值范围;
的取值范围;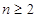 且
且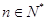 时,证明:
时,证明: 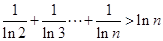 .
.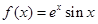 函数.
函数.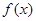 单调递增区间;
单调递增区间;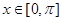 时,求函数
时,求函数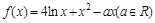 .
.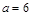 时,求函数
时,求函数 的单调区间;
的单调区间;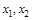 ,且
,且 ,求证:
,求证: ;
;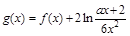 ,对于任意
,对于任意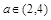 时,总存在
时,总存在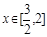 ,使
,使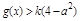 成立,求实数
成立,求实数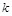 的取值范围.
的取值范围.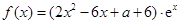 (
(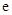 为自然对数的底数).
为自然对数的底数).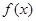 在
在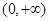 上的单调区间;
上的单调区间;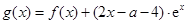 ,是否存在区间
,是否存在区间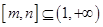 ,使得当
,使得当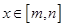 时函数
时函数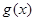 的值域为
的值域为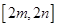 ,若存在求出
,若存在求出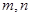 ,若不存在说明理由.
,若不存在说明理由.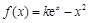 (其中
(其中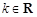 ,e是自然对数的底数).
,e是自然对数的底数).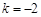 ,试判断函数
,试判断函数 在区间
在区间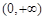 上的单调性;
上的单调性;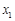 ,
,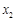 (
(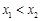 ),求k的取值范围;
),求k的取值范围;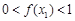 .
.