题目内容
19．（1+2x）（1+x）5的展开式中x2的系数是20．分析 利用二项式定理的通项公式即可得出．
解答 解：（1+x）5展开式的通项为${T_{r+1}}=C_5^r{x^r}$，
由题意可知，x2的系数为$1×C_5^2+2×C_5^1=20$．
故答案为：20．
点评 本题考查了二项式定理的应用，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
14．已知数列{an}满足2Sn=4an-1．则log2a3与log2a9的等差中项为（ ）
| A． | 5 | B． | 4 | C． | 3 | D． | 2 |
4．已知变量x，y满足约束条件$\left\{{\begin{array}{l}{x+y-1≤0}\\{x-y-1≤0}\\{x-a≥0}\end{array}}\right.$，若$|{\frac{y}{x-2}}|≤\frac{1}{2}$，则实数a的取值范围是（ ）
| A． | （0，1] | B． | [0，1） | C． | [0，1] | D． | （0，1） |
如图，已知正三棱柱ABC-A1B1C1的体积为$9\sqrt{3}$，底面边长为3，求异面直线BC1与AC所成的角的大小．
8．函数f（x）=2sin（ωx+φ）（w＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则f（0）+f（$\frac{17π}{12}$）的值为（ ）
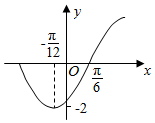
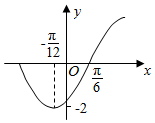
| A． | 2-$\sqrt{3}$ | B． | 2+$\sqrt{3}$ | C． | 1-$\frac{\sqrt{3}}{2}$ | D． | 1+$\frac{\sqrt{3}}{2}$ |