题目内容
a，b为非零向量，“函数f(x)＝(
ax＋b)2为偶函数”是“a⊥b”的( )
(A)充分不必要条件 (B)必要不充分条件(C)充要条件 (D)既不充分也不必要条件
C.f(x)＝a2x2＋2a·bx＋b2，∵a、b为非零向量，若f(x)为偶函数，则f(－x)＝f(x)恒成立，∴a2x2－2a·bx＋b2＝a2x2＋2a·bx＋b2，∴4a·bx＝0，又x∈R，∴a·b＝0，∴a⊥b；
若a⊥b，则a·b＝0，∴f(x)＝a2x2＋b2，∴f(x)为偶函数.
综上，选C.
练习册系列答案
名校课堂系列答案
相关题目
的各项均为正数，
，前
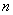项和为
，
为等比数列，
，且
，
。
与
的通项公式 （2） 求
的前
项和为
且满足
则
中最大的项为 （ ）
是圆
：
上的两个点，
是
线段上的动点，当
的面积最大时，则
的最大值是（ ） 
D. 
为单位向量，且
，
=1，则
； ⑵若
=0，则
； ⑷若
，则必有
； ⑸若
，则
△ABC的面积
夹角的取值范围是（ ）
B．
C．
D．
已知△ABC为等边三角形，AB=2．设点P，Q满足
，
，λ∈R．若
=﹣
，则λ=（ ）
|
| A． |
| B． |
| C． |
| D． |
|
中，
，
，且
，则
的最大值为（ ）
B．
C．
D．
＝0，则△ABC是( )．