题目内容
抛物线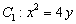 在点
在点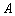 ,
,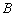 处的切线垂直相交于点
处的切线垂直相交于点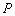 ,直线
,直线 与
与
椭圆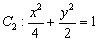 相交于
相交于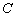 ,
,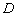 两点.
两点.
(Ⅰ)求抛物线 的焦点
的焦点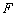 与椭圆
与椭圆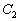 的左焦点
的左焦点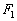 的距离;
的距离;
(Ⅱ)设点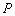 到直线
到直线 的距离为
的距离为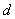 ,试问:是否存在直线
,试问:是否存在直线 ,使得
,使得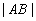 ,
,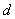 ,
,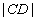
成等比数列?若存在,求直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
 |
(I)解:抛物线 的焦点
的焦点 , …
, …
椭圆 的左焦点
的左焦点 ,
,
则 .
.
(II)解:设直线 ,
, ,
, ,
, ,
, ,
,
由 ,得
,得 ,
,
故 ,
, .
.
由 ,得
,得 ,故切线
,故切线 ,
, 的斜率分别为
的斜率分别为 ,
, ,
,
再由 ,得
,得 ,即
,即 ,
,
故 ,这说明直线
,这说明直线 过抛物线
过抛物线 的焦点
的焦点 .
.
由 ,得
,得 ,
,
 ,即
,即 .
.
于是点 到直线
到直线 的距离
的距离 .
.
由 ,得
,得 ,
,
从而 ,
,
同理, .
.
若 ,
,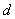 ,
, 成等比数列,则
成等比数列,则 ,
,
即 ,化简整理,得
,化简整理,得 ,
,
此方程无实根,所以不存在直线 ,使得
,使得 ,
,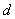 ,
, 成等比数列.
成等比数列.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 是边长为1的正方形内的一点,若
是边长为1的正方形内的一点,若 ,
, ,
, ,
, 面积均不小于
面积均不小于 ,则
,则 的最大值为 .
的最大值为 .
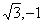 ),n=(cosA,sinA).若m⊥n,且acosB+bcosA=csinC,则角B=__ __.
),n=(cosA,sinA).若m⊥n,且acosB+bcosA=csinC,则角B=__ __. 右支上一点,
右支上一点, 的中垂线,则该双曲线的离心率是( )
的中垂线,则该双曲线的离心率是( ) B.
B.  C.
C.  D.
D. 
 ,
, ,
, 满足
满足 ,
, ,
, ,
, ,则
,则 的最小值为 .
的最小值为 . 与两坐标轴无公共点,那么实数
与两坐标轴无公共点,那么实数 的取值范围是
的取值范围是 
 B.
B. C.
C.  D.
D.
 ,和直线
,和直线 相切,且
相切,且 圆心在直线
圆心在直线 上的圆方程.(12分)
上的圆方程.(12分) 是
是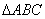 内的一点,且
内的一点,且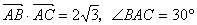 。定义:
。定义:
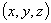 ,其中
,其中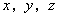 分别为
分别为 的面积,若
的面积,若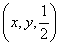 ,则
,则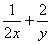 的最小值为______________________,此时
的最小值为______________________,此时 项之和
项之和 为,且前
为,且前 ,则前
,则前 B.
B. C.
C. D.
D.