题目内容
5.已知函数f(x)=$\frac{1}{3}{x^3}$-$\frac{b}{2}{x^2}$+x+d在R上单调,则b的取值范围为[-2,2].(用区间表示)分析 函数f(x)=$\frac{1}{3}{x^3}$-$\frac{b}{2}{x^2}$+x+d在R上单调,f′(x)≥0恒成立,利用判别式,即可得出结论.
解答 解:∵f(x)=$\frac{1}{3}{x^3}$-$\frac{b}{2}{x^2}$+x+d,
∴f′(x)=x2-bx+1
∵函数f(x)=$\frac{1}{3}{x^3}$-$\frac{b}{2}{x^2}$+x+d在R上单调,
∴f′(x)≥0恒成立,
∴b2-4≤0,
∴-2≤b≤2.
故答案为:[-2,2].
点评 本题主要考查函数单调性和导数之间的关系,将函数在R上单调递增转化为f′(x)≥0恒成立是解决本题的关键.

练习册系列答案
相关题目
10.过点(1,-1)且与曲线y=x3-2x相切的切线方程为( )
| A. | x-y-2=0或5x+4y-1=0 | B. | x-y-2=0 | ||
| C. | x-y+2=0 | D. | x-y-2=0或4x+5y+1=0 |
17.与曲线y=x2相切,且与直线x+2y+1=0,垂直的直线的方程为( )
| A. | y=2x-2 | B. | y=2x+2 | C. | y=2x-1 | D. | y=2x+1 |
15.下列函数中,在(0,$\frac{π}{2}$)内单调递增,且以π为最小正周期的偶函数是( )
| A. | y=tan|x| | B. | y=|tanx| | C. | y=cot|x| | D. | y=|cotx| |
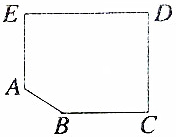 某小区内有一块荒地ABCDE,今欲在该荒地上划出一块长方形地面(不改变方位)进行开发(如图所示),问如何设计才能使开发的面积最大?最大开发面积是多少?(已知BC=210m,CD=240m,DE=300m,EA=180m)
某小区内有一块荒地ABCDE,今欲在该荒地上划出一块长方形地面(不改变方位)进行开发(如图所示),问如何设计才能使开发的面积最大?最大开发面积是多少?(已知BC=210m,CD=240m,DE=300m,EA=180m)