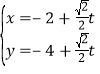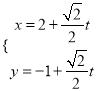题目内容
【题目】盒子中装有四张大小形状均相同的卡片,卡片上分别标有数![]() 其中
其中![]() 是虚数单位.称“从盒中随机抽取一张,记下卡片上的数后并放回”为一次试验(设每次试验的结果互不影响).
是虚数单位.称“从盒中随机抽取一张,记下卡片上的数后并放回”为一次试验(设每次试验的结果互不影响).
(1)求事件![]() “在一次试验中,得到的数为虚数”的概率
“在一次试验中,得到的数为虚数”的概率![]() 与事件
与事件![]() “在四次试验中,
“在四次试验中,
至少有两次得到虚数” 的概率![]() ;
;
(2)在两次试验中,记两次得到的数分别为![]() ,求随机变量
,求随机变量![]() 的分布列与数学期望
的分布列与数学期望![]()
【答案】(1) ![]() (2)见解析
(2)见解析
【解析】试题分析:(1)根据卡片上分别标有数﹣i,i,﹣2,2其中i是虚数单位,可求P(A),利用对立事件的概率公式,可求P(B);
(2)确定随机变量ξ=|ab|的取值,求出相应的概率,可得分布列与数学期望Eξ.
试题解析:
(1)∵卡片上分别标有数﹣i,i,﹣2,2其中i是虚数单位,
∴P(A)=![]() =
=![]() ,
,
P(B)=1﹣P(![]() )=1﹣[
)=1﹣[![]() ]=1﹣
]=1﹣![]() =
=![]()
(2)a,b,ξ的可能取值如下表所示:

由表可知:P(ξ=1)=![]() =
=![]() ,P(ξ=2)=
,P(ξ=2)=![]() =
=![]() ,P(ξ=4)=
,P(ξ=4)=![]() =
=![]()
∴随机变量ξ的分布列为

∴Eξ=1×![]() +2×
+2×![]() +4×
+4×![]() =
=![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目